神戸女学院中学部1992年算数2日目第3問(解答・解説)
(1)
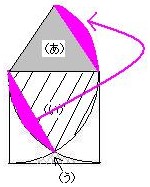
図のように等積移動を行います。
すると、求める面積の和は、半径10cm、中心角120度の扇形になるので、
10×10×3.14×1/3
=314/3cm2(104と2/3cm2)
(2)
(解法1)「A−B→(A+C)−(B+C)」・・・(★)を利用します。
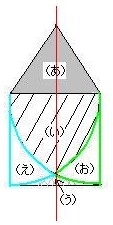
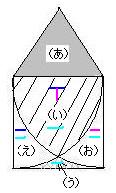
問題の図は、図の赤線に関して対称だから、(え)と(お)の面積は等しくなります。
すると、求める面積の差
(い)−(う)
={(い)+(え)}−{(う)+(お)}
=(1辺10cmの正方形の面積)×(100+57−43)/200 ←(花びらの面積について)を参照しましょう。
=10×10×114/200
=100×57/100
=57cm2
実は、求める面積は、花びらの面積(正方形の面積の57/100倍)になっています。
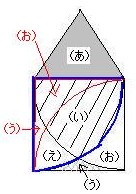
このことは、下の図のように、{(い)+(え)}の図形(青線で囲んだ扇形)と{(う)+(お)}の図形(赤線で囲んだ図形)を重ね合わせてみると、すぐにわかります。
(★)「A−B→(A+C)−(B+C)」
AとBの差を考える場合に、同じもの(C)をA、Bそれぞれに付け足して考えるというのは、図形問題以外でも利用できます。
例えば、次のような計算の場合にも利用できます。
3・46/99−98/99 ←帯分数をなかぐろ(・)を用いて表記しています。
=(3・46/99+1/99)−(98/99+1/99)
=3・47/99−1
=2・47/99(実際は、暗算で解けますね!)
(花びらの面積について)
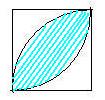
花びらの面積(花びらの面積の基本図1の水色の斜線部分)
=(1/4円の面積)+(1/4円の面積)−(正方形の面積) ←「たしすぎたら、ひく」
=(半径)×(半径)×(円周率)×1/4×2−(半径)×(半径)
=(半径)×(半径)×{(円周率)/2−1} 分配法則の逆を利用しました。
特に、円周率が3.14のときは、
(半径)×(半径)×(3.14/2−1)
=(半径)×(半径)×0.57
となります。
円周率が3.14のとき
(正方形の面積):(花びらの面積):{(正方形の面積)−(花びらの面積)}
=(半径)×(半径):(半径)×(半径)×0.57:{(半径)×(半径)−(半径)×(半径)×0.57}
=1:0.57:0.43
=100:57:43
また、それぞれを半分にした面積比も同様になります。
(直角二等辺三角形の面積):(花びらの半分の面積):(図の紫色の斜線部分の面積)
=100:57:43
なお、花びらの半分の面積を求めてから、2倍することにより花びらの面積を求めることもできます。
(解法2)うまく足し引きして解きます。
結局、花びらの面積を求める手法と同じ解法ですが、花びらの面積についての知識がないということを前提として解いていきます。
上の図の色線は、それぞれの箇所のカウント回数を「正」の字を書く要領で書き込んだものです(たす場合とひく場合を分けてカウントしています)。
(い)−(う)
= (1/4円の面積)・・・(い)1個 (え)1個 〜青色
+(1/4円の面積)・・・(い)1個 (お)1個 〜紫色
−(1辺10cmの正方形の面積)・・・(い)1個 (え)1個 (お)1個 (う)1個 〜水色
=10×10×3.14×1/4×2−10×10
=10×10×1.57−100
=157−100
=57cm2