洛南高校附属中学校2009年算数第3問(解答・解説)
相似を使うまでもないですね。
(1)
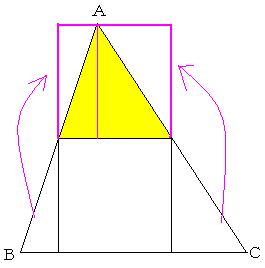
図のように三角形を移動すると、正方形の1つ目の正方形の面積が三角形ABCの面積の1/2となることは一目瞭然ですね。
黄色の三角形の部分(三角形ABCの面積の1/4(1/2の1/2))で全く同じ作業をすることになるので、2つ目の正方形の面積は、三角形ABCの面積の1/8(1/4の1/2)となります。
したがって、
(三角形ABCの面積):(2つの正方形の面積の和)
=1:(1/2+1/8)
=1:(4+1)/8
=8:5
となります。
(2)
図2の1番上の三角形(面積は、三角形ABCの面積の1/16(1/8の1/2)のところで、同様の作業をするだけなので、3つ目の正方形の面積は、三角形ABCの面積の1/32(1/16の1/2)となります。
したがって、
(三角形ABCの面積):(3つの正方形の面積の和)
=1:(1/2+1/8+1/32)
=1:(16+4+1)/32
=32:21
となります。
なお、次のような規則になることはすぐにわかりますね。
1つ目の正方形の面積 三角形ABCの面積の1/2
↓×1/4
2つ目の正方形の面積 三角形ABCの面積の1/8
↓×1/4
3つ目の正方形の面積 三角形ABCの面積の1/32
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・