清風南海中学校2003年1次算数第8問(解答・解説)
球の体積などという「はったり」に惑わされないようにしましょう。
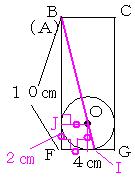
右から見た図を描きます。 ←立体の問題は平面で考えるのが基本ですね。
ちょうど長方形の中に円がきっちりと入っている状態と同じになりますね。
三角形BJOと三角形BFIのピラミッド相似(相似比は、BJ:BF=(10−2):10=4:5)に注目すると、
FI
=JO×5/4
=2×5/4
=5/2cm
となり、
IG
=4−5/2
=3/2cm
となります。
求める体積は、底面が台形BIGCで、高さGHの四角柱の体積から、球の体積の半分((*)を参照)を引いたものだから、
(4+3/2)×10×1/2×4−4/3×2×2×2×22/7×1/2 ←円周率が22/7であることに注意しましょう。
=11/2×10×1/2×4−4/3×2×2×2×22/7×1/2
=110−352/21
=1958/21cm2
となります。
(*)「点対称図形(平面図形)は、点対称の中心を通るどのような直線によっても2等分される」というのがありますが、これは、立体図形(「点対称図形は、点対称の中心を通るどのような平面によっても2等分される」)でも成り立ちます。
球は明らかに点対称図形だから、球の中心Oを通るどのような平面によっても球は2等分されることがわかりますね。