巐揤墹帥拞妛峑侾俋俋俉擭嶼悢俛戞俆栤乮夝摎丒夝愢乯
乮侾乯
妏搙偺榓傪媮傔傞栤戣偱偡丅
妏搙偺榓傪媮傔傞栤戣偱偼丄妏搙傪侾偮偺応強偵廤傔傞偺偑億僀儞僩偱偡丅
偙偺栤戣偺応崌丄嶰妏宍偺奜妏偑偨偔偝傫偁傝傑偡偹丅
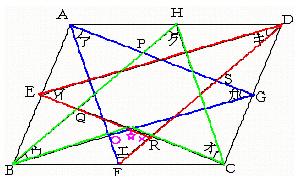
傑偢惵偄晹暘乮嶰妏宍偺奜妏乯偵拲栚偡傞偲丄乑偑
丂丂傾亄僇
偵側偭偰偄傞偙偲偑傢偐傝傑偡丅
師偵愒偄晹暘乮嶰妏宍偺奜妏乯偵拲栚偡傞偲丄亊偑
丂丂僀亄僉
偵側偭偰偄傞偙偲偑傢偐傝傑偡丅
嵟屻偵墿椢怓偺晹暘乮僽乕儊儔儞乣乮仚乯傪嶲徠乯偵拲栚偡傞偲丄仚偑
丂丂僂亄僆亄僋
偵側偭偰偄傞偙偲偑傢偐傝傑偡丅
寢嬊丄傾乣僋偺俉偮偺妏偺崌寁偼丄巐妏宍偺撪妏偺榓偵側偭偰偄傞偐傜丄
丂丂俁俇侽搙
忋偺夝朄偱偼丄僄偺偲偙傠偵妏傪廤傔傑偟偨偑丄僄埲奜偺偲偙傠偵廤傔傞偙偲傕偱偒傑偡丅
乮仚乯
乮暿夝乯
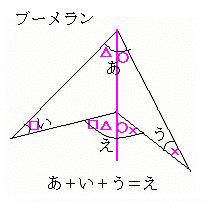
傾乣僋偺俉偮偺妏偺崌寁偑丂丂乽偨偟偡偓偨傜丄傂偔乿
丂丂丂嶰妏宍俛俧俹偺撪妏偺榓
丂丂亄嶰妏宍俠俫俻偺撪妏偺榓
丂丂亄嶰妏宍俛俼俢偺撪妏偺榓
丂丂亄嶰妏宍俥俽俙偺撪妏偺榓
丂丂亅暯峴巐曈宍乮巐妏宍乯俹俻俼俽偺撪妏偺榓
偵側偭偰偄傞偙偲傪棙梡偟偰丄
丂丂侾俉侽亊係亅侾俉侽亊俀
丂亖侾俉侽亊乮係亅俀乯
丂亖俁俇侽搙
偲偟偰傕偄偄偱偟傚偆丅
巐揤偺弌戣幰偺堄恾偼偨傇傫偙偪傜偺夝朄偱偟傚偆偹丅
乮俀乯
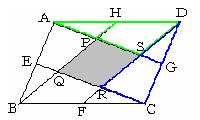
暯峴巐曈宍俹俻俼俽傪暘抐偡傞捈慄俢俤丄俛俧丄俙俥丄俠俫傪彍偄偨恾傪昤偔偺偑偄偄偱偟傚偆丅
墿椢怓偺僺儔儈僢僪憡帡乮嶰妏宍俙俹俫偲嶰妏宍俙俽俢乯偵拲栚偡傞偲
丂丂俹俫丗俽俢亖侾丗俀
偩偐傜丄俹俫亖嘆偲偡傞偲丄俽俢亖嘇偲側傝傑偡丅
偙偙偱丄惵怓偺僺儔儈僢僪憡帡乮嶰妏宍俢俽俧偲嶰妏宍俢俼俠乯偵拲栚偡傞偲
丂丂俢俽丗俽俼
亖俢俽丗乮俢俼亅俢俽乯
亖侾丗乮俀亅侾乯亖侾丗侾
偩偐傜丄俽俼亖嘇偲側傝傑偡丅
傑偨忋偺恾宍偑揰懳徧恾宍偱偁傞偙偲偵拲栚偡傞偲
丂丂俼俥亖俹俫亖嘆丂丂丂懳徧惈傪棙梡偟偰嶌嬈傪尭傜偡両両
丂丂俹俻亖俽俼亖嘇
丂丂俻俛亖俽俢亖嘇
偁偲偼丄乮暯峴慄偲柺愊斾乯偺抦幆傪棙梡偡傞偩偗偱偡丅
丂丂暯峴巐曈宍俹俻俼俽偺柺愊
丂亖暯峴巐曈宍俫俛俥俢偺柺愊亊乮嘇亊俀乯/乷乮嘆亄嘇亄嘇乯亊俀乸
丂亖暯峴巐曈宍俫俛俥俢偺柺愊亊俀/俆
丂亖暯峴巐曈宍俙俛俠俢偺柺愊亊乮侾亊俀乯/乮俀亊俀乯亊俀/俆
丂亖暯峴巐曈宍俙俛俠俢偺柺愊亊侾/俆
偩偐傜丄
丂丂暯峴巐曈宍俹俻俼俽偺柺愊丗暯峴巐曈宍俙俛俠俢偺柺愊
丂亖侾丗俆
乮暯峴慄偲柺愊斾乯
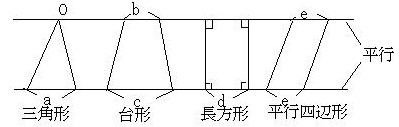
壓偺恾偺柺愊斾偼丄偄偢傟傕乽忋掙亄壓掙乿偺斾偱張棟偱偒傑偡乮挿曽宍傕暯峴巐曈宍傕戜宍偩偐傜丄嵍偺俀偮偱偡傋偰張棟偱偒傑偡丅傑偨丄嶰妏宍傪忋掙侽偺戜宍偲峫偊傞偲丄偡傋偰傪戜宍偲偟偰張棟偱偒傑偡偹乯丅
柺愊斾偼
丂丂乮a亄侽乯丗乮倐亄們乯丗乮倓亄倓乯丗乮e亄e乯
偲側傝傑偡丅
乮暿夝乯
暯峴巐曈宍偺摿庩側応崌乮惓曽宍乯偱峫偊傞偲丄娙扨偵夝偗傑偡丅
棟榑揑偵偼惓偟偔偼側偄偱偡偑丄摎偊偼媮傑傝傑偡丅
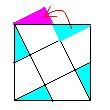
恾偺悈怓偺晹暘偺捈妏嶰妏宍傪恾偺愒巼怓偺晹暘偵堏摦偡傞乮懳徧惈偵傛傝丄懠偺悈怓偺晹暘傕摨條偵偱偒傑偡乯偲丄恾偺拞偺戝偒側惓曽宍偼彫偝側惓曽宍俆屄暘偵側偭偰偄傞偙偲偑傢偐傝傑偡偹丅