麻布中学校2023年算数第2問(解答・解説)
(1)
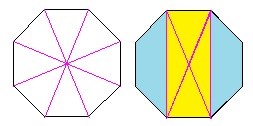
正八角形は8個の合同な三角形に分けることができ、また、長方形の面積は2本の対角線によって面積が等しい4個の三角形に分けられるから、黄色の長方形の面積は正八角形の面積の4/8=1/2倍となります。 ←水色の台形1つの面積は正八角形の面積の(1−1/2)×1/2=1/4倍となります。一般に、正N角形(Nは偶数)の対辺を2辺とする長方形の面積は正N角形の面積の4/Nとなります(正八角形の場合と同じように考えればすぐにわかりますね)。このことに関する問題は過去に算数オリンピックやジュニア算数オリンピックで何度か出されています。
三角形PABと三角形PEFの面積の和は、長方形ABEFの面積の半分となるから、30×1/2×1/2=15/2cm2となります。
(2)
(1)と同じ図を作出するため、図のように補助線を引きます。
(1)と同様に考えると、オレンジ色の部分の面積と黄緑色の部分の面積はともに15/2cm2となります。
また、四角形ABCQの面積が30×1/3=10cm2となるから、四角形QEFGの面積は
15/2×2−10
=5cm2
となり、三角形QERの面積は
5×1/(1+3)
=5/4cm2
となり、四角形QCDEの面積は
10−5/4
=35/4cm2
となります。