麻布中学校2024年算数第2問(解答・解説)
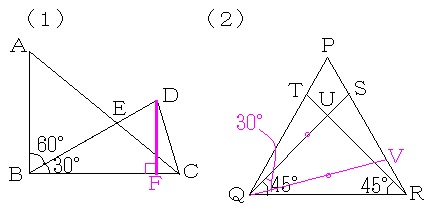
(1)
三角形ABEの面積−三角形CDEの面積
=三角形ABCの面積−三角形BCDの面積 ←引かれる数と引く数に共通部分の三角形BCEの面積を加えても差は変わりませんね。
=6×5×1/2−6×3×1/2 ←正三角形を半分にした三角定規の辺の比に関する知識((参考)を参照)を利用すると、DFの長さが6×1/2=3cmとなることはすぐにわかりますね。
=6cm2
となります。
(2)
三角形UQRの面積−四角形PTUSの面積
=三角形SQRの面積−三角形SPQの面積 ←引かれる数と引く数に共通部分の三角形TQUの面積(=三角形SRUの面積)を加えても差は変わりませんね。
=三角形QVSの面積 ←2つの図形の面積の差を求めるのだから、2つの図形を重ね合わせて面積の差がどの面積になるかあぶりだしました。面積の差を求める問題では、同じものを足し引きする手法だけでなく、2つの図形を重ね合わせて面積の差をあぶりだす手法をしっかりマスターしておきましょう(神戸女学院中学部1992年算数2日目第3問)の解答・解説を参照)。
=5×5/2×1/2 ←正三角形を半分にした三角定規の辺の比に関する知識((参考)を参照)を利用しました。(1)の三角形BCDの面積の(5×5)/(6×6)倍としてもよいでしょう。
=25/4cm2
となります。
(参考)正三角形を半分にした三角定規の辺の比に関する知識とその知識を利用した面積公式(いわゆる30度問題、150度問題)
正三角形を半分にした三角定規では、一番長い辺と一番短い辺の長さの比が2:1になります。
このことを利用すると、次の面積公式が導かれます。
一般に、三角形の2辺(□と○)をはさむ角度が30度、150度のとき、三角形の面積は
□×(○×1/2)×1/2
=□×○×1/4
となります。
30゚、150゚の角度が登場する場合は、上の公式を思い浮かべるとよいでしょう。特に、上の三角形が○=□の二等辺三角形となる場合は、(180゚−30゚)÷2=75゚、(180゚−150゚)÷2=15゚が登場するので、75゚、15゚の角度が登場する場合も、上の公式を思い浮かべるとよいでしょう。