一橋大学2024年数学第5問(解答・解説)
条件を満たす三角形は鋭角三角形ですね。
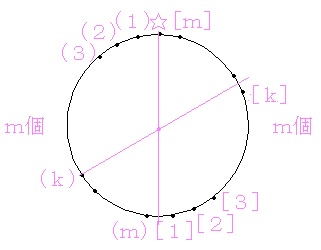
nを2×m+1(mは1以上の整数)とし、三角形の1つの頂点を固定(図の☆)し、残り2つの頂点を選ぶと考えます。 ←ダブりを防ぐためです。
残りの2×m個の頂点を正n角形の線対称の軸によってm個ずつ分け、図のように記号を付けます。 ←この問題の場合、どの線対称の軸によっても、線対称の軸を通る頂点以外の2×m個の頂点はm個ずつに分けられますね。このことは後で使います。
右側のm個の頂点だけから(もちろん左側のm個の頂点だけからも)2個選ぶと条件を満たさないことは明らかだから、左側のm個の頂点の場所を固定したときに、残り1つの頂点の場所がどこになるか考えていきます。
その際、正n角形の線対称の軸に着目します。 ←nが奇数で、円の直径を通る2頂点はないから、直角三角形となることはありえず、鈍角三角形を避ければいいですね。ただし、鈍角三角形を意識しながら、鋭角三角形を直接数え上げていきます。
(1)のときは、[1]の1個
(2)のときは、[1]、[2]の2個
(3)のときは、[1]、[2]、[3]の3個
・・・・・・・・・・・・・・・・・・・・・・・・・・
(k)のときは、[1]、[2]、[3]、・・・[k]のk個 ←(m−k)個と何個かでm個だから、k個となることが分かりますね。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
(m)のときは、[1]、[2]、[3]、・・・、[m]のm個
だから、条件を満たす2頂点の選び方は
1+2+3+・・・+m
={1+(n−1)/2}×(nー1)/2×1/2 ←等差数列の和の公式を利用しました。その際、n=2×m+1を逆算して、m=(n−1)/2となることを利用しました。
=(n+1)×(n−1)/8(通り)
あります。
残り2頂点の選び方は全部で
(n−1)×(n−2)/(2×1) ←組合せですね。
=4×(n−1)×(n−2)/8(通り) ←比率をわかりやすくするために、このように変形しました。
あるから、求める確率は(n+1)/{4×(n−2)}となります。
なお、わかりにくければ、具体例(正五角形、正七角形の場合など)を考えてみればよいでしょう。因みに、正三角形の場合は、頂点の選び方は1通りに定まり、必ず鋭角三角形なるので、確率は1というつまらない場合になりますが、上の説明は成り立ちます。
nが奇数と指定されていない問題が1966年に京都大学で出されているので、ぜひ解いてみましょう。