恄屗戝妛俀侽俀係擭棟宯悢妛戞俁栤乮夝摎丒夝愢乯
乮侾乯
侾丄俀丄俁丄係丄俆丄俇偺偄偢傟偺栚偑弌偰傕値偺栺悢偲側傞偲偄偆偙偲偩偐傜丄丄値偑侾丄俀丄俁丄係丄俆丄俇偺攞悢偲側偭偰偄傞丄偮傑傝丄値偑侾丄俀丄俁丄係丄俆丄俇偺嵟彫岞攞悢偺攞悢偲側偭偰偄傞偲偄偆偙偲偱偡偹丅
侾偼偁傜備傞惍悢偺栺悢偩偐傜峫椂偡傞昁梫偼偁傝傑偣傫丅
俀丄俁偼俇偵娷傑傟傞偺偱丄係丄俆丄俇偺嵟彫岞攞悢傪峫偊傟偑偄偄偱偡偹丅
係丄俆丄俇偺嵟彫岞攞悢偼係亊俆亊俁亖俇侽偩偐傜丄媮傔傞値偼彫偝偄弴偵俇侽丄侾俀侽丄侾俉侽偲側傝傑偡丅
乮俀乯
栤戣偺忦審偼丄俇偮偺栚偺偆偪侾偮偺栚偩偗偑値偺栺悢偲側偭偰偄側偄偲偄偆偙偲偱偡偹丅
侾偼偁傜備傞惍悢偺栺悢偩偐傜丄侾乮偩偗乯偑値偺栺悢偲側傜側偄偙偲偼偁傝偊傑偣傫丅
俀偑値偺栺悢偱側偗傟偽丄俇傕値偺栺悢偱側偔側傞偺偱丄俀偩偗偑値偺栺悢偲側傜側偄偙偲偼偁傝偊傑偣傫丅
俁偑値偺栺悢偱側偗傟偽丄俇傕値偺栺悢偱側偔側傞偺偱丄俁偩偗偑値偺栺悢偲側傜側偄偙偲偼偁傝偊傑偣傫丅
係偩偗偑値偺栺悢偱側偄偙偲偼偁傝偊傑偡丅丒丒丒乮偁乯
俆偩偗偑値偺栺悢偱側偄偙偲偼偁傝偊傑偡丅丒丒丒乮偄乯
俇偑値偺栺悢偱側偗傟偽丄値偼俀傑偨偼俁偺彮側偔偲傕堦曽傪栺悢偲偟偰帩偨側偄偙偲偵側傞偺偱丄俇偩偗偑値偺栺悢偲側傜側偄偙偲偼偁傝偊傑偣傫丅
乮偁乯偺応崌
値偼侾丄俀丄俁丄俆丄俇偺攞悢乮偨偩偟丄係偺攞悢埲奜乯偲側偭偰傑偡丅
乮侾乯偲摨條偵峫偊傞偲丄値偼俁侽偺攞悢乮偨偩偟丄俁侽亊婏悢乯偲側傝丄俁侽丄俋侽丄侾俆侽偑
摎偊偺岓曗偲側傝傑偡丅
乮偄乯偺応崌
値偼侾丄俀丄俁丄係丄俇偺攞悢乮偨偩偟丄俆偺攞悢埲奜乯偲側偭偰傑偡丅
乮侾乯偲摨條偵峫偊傞偲丄値偼侾俀偺攞悢乮偨偩偟丄侾俀亊俆偱妱傝愗傟側偄悢乯偲側傝丄侾俀丄俀係丄俁俇偑摎偊偺岓曗偲側傝傑偡丅
乮偁乯丄乮偄乯傛傝丄媮傔傞値偼彫偝偄弴偵侾俀丄俀係丄俁侽偲側傝傑偡丅
乮俁乯
偡傋偰偺応崌偼丄俇亊俇亊俇乮捠傝乯偁傝傑偡偹丅
侾俇侽亖係亊係亊侾侽亖俀亊俀亊俀亊俀亊俀亊俆偲側傝傑偡丅
僒僀僐儘偺栚乮侾埲奜乯傪慺場悢暘夝偟偨偲偒偵尰傟傞慺場悢偼俀丄俁丄俆偩偗偱偡偹丅
乮傾乯侾俇侽偼慺場悢俁傪帩偨側偄偐傜丄俁偲俇偺栚偑弌側偄偙偲偵側傝傑偡丅
乮僀乯侾俇侽偼慺場悢俆傪侾屄偟偐帩偨側偄偐傜丄俆偺栚偼侾夞埲壓偟偐弌側偄偙偲偵側傝傑偡丅
乮僂乯侾俇侽偼慺場悢俀傪俆屄偟偐帩偨側偄偐傜丄係偺栚偼俀夞埲壓偟偐弌側偄偙偲偵側傝傑偡丅
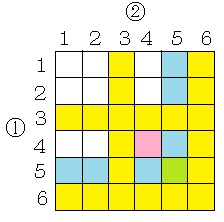
僒僀僐儘傪俁夞傆傞栤戣偩偐傜丄侾夞栚乮嘆乯偲俀夞栚乮嘇乯偵弌偨栚偵偮偄偰偼丄俇亊俇偺昞傪偐偒丄俁夞栚乮嘊乯偵弌偨栚偵偮偄偰偼丄僽儘僢僋傪愊傒忋偘傞僀儊乕僕偱張棟偟傑偡丅
墿怓偺奺晹暘偼丄乮傾乯偵傛傝丄侽捠傝偲側傝傑偡丅
墿椢怓偺晹暘偼丄乮僀乯偵傛傝丄侽捠傝偲側傝傑偡丅
悈怓偺奺晹暘偼丄乮僀乯丄乮傾乯偵傛傝丄嘊偼俆丄俁丄俇埲奜偺俁捠傝偁傝傑偡丅
僺儞僋怓偺晹暘偼丄乮僂乯丄乮傾乯偵傛傝丄嘊偼係丄俁丄俇埲奜偺俁捠傝偲側傝傑偡丅
敀怓偺奺晹暘偼丄乮傾乯偵傛傝丄嘊偼俁丄俇埲奜偺係捠傝偁傝傑偡丅
寢嬊丄忦審傪枮偨偡応崌偼慡晹偱
丂丂俁亊俇亄俁亄係亊俉
丂亖俆俁捠傝
偁傞偐傜丄媮傔傞妋棪偼俆俁/俀侾俇偲側傝傑偡丅