大阪大学1999年前期理系数学第5問(解答・解説)
すべての場合は
(16×15)/(2×1)×(16×15)/(2×1) ←A、Bそれぞれが16個のマス目から異なる2個のマス目を選ぶからです。
=120×120(通り)
あります。
条件を満たす場合について考えます。
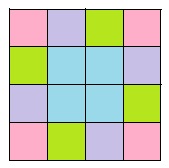
頭の中で、4×4のマス目を点対称の中心の周りに90度ずつ回転すると、図の同じ色を付けた部分(4色ありますね)がすべて条件的に同じことがわかります。 ←条件の対等性の利用
条件を満たすのは、Aが選んだマス目とBが選んだマス目に同じ色のものがないときだけになります。
次の2つの場合に分けて考えます。
(あ)Aが選んだ2個のマス目が同じ色の場合
(い)Aが選んだ2個のマス目が異なる色の場合
(あ)の場合
Aが4色のうちどの1色のマス目を選ぶかで4通りあり、そのそれぞれに対して、4個のマス目のうちどの2個のマス目を選ぶかで(4×3)/(2×1)=6通りあり、そのそれぞれに対して、Bが12個のマス目のうちどの2個のマス目を選ぶかで(12×11)/(2×1)=66通りあるから、この場合は4×6×66(通り)あります。 ←Bがマス目を選ぶ際、Aが選んだ色のマス目がつぶれてなくなっていることに注意しましょう(以下、同じ)。
(い)の場合
Aが4色のうちどの2色のマス目を選ぶかで(4×3)/(2×1)=6通りあり、そのそれぞれに対して、選んだ色のマス目4個のうちどの1個のマス目を選ぶかで4×4(通り)あり、そのそれぞれに対して、Bが8個のマス目のうちどの2個のマス目を選ぶかで(8×7)/(2×1)=28通りあるから、この場合は6×4×4×28(通り)あります。
したがって、求める確率は
(4×6×66+6×4×4×28)/(120×120)
=(66+4×28)/(30×20) ←まず4×6で約分しました。
=(33+56)/300
=89/300
となります。