京都大学1998年前期文理共通数学第5問(解答・解説)
(1)
9個から3個の玉の取り出し方は全部で
(9×8×7)/(3×2×1) ←組合せですね。
=84通り
あり、A(0)、A(1)、A(2)、A(3)を合計したものになります。
高得点のほうがなさそうなので、A(3)から考えていきます。
A(3)について
色も番号も異なる3個の玉を取り出したということですね。
青色の玉の番号については3通りあり、そのそれぞれに対して、赤色の玉の番号は青色の玉の番号以外の2通りあり、そのそれぞれに対して、白色の玉の番号は赤色と青色の玉の番号以外の1通りあるから、全部で
3×2×1
=6通り
あり、A(3)=6となります。
A(2)について
得点を失うのは、色が同じものや番号が同じもの同士でつぶしあう感じですね。 ←問題文の例からもすぐにわかりますね。
得点を失う場合、当然1点だけ失うことはなく、少なくとも2点失うことになるから、この場合はありえず、A(2)=0となります。
A(1)について
どの玉で点を得たか考えると9通り考えられますね。
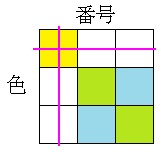
いずれの場合においても、この玉と同じ色の玉も同じ番号の玉も使うことができなくなるので、2×2=4個の玉から残り2個の玉を選ぶことになります。 ←下のイメージ図(黄色の部分が点を得た玉、黄緑色の部分と水色の部分が残り2個の玉を選ぶところで、水色の部分のペアと黄緑色の部分のペアが条件を満たさない組合せになります)を参照。
(4×3)/(2×1)
=6通り
のうち、番号も色も異なる2通りの場合のみ条件を満たさないから、結局、この場合は9×(6−2)=36通りあり、A(1)=36となります。
A(0)について
A(0)=84−(6+0+36)=42となります。
(2)
平均を計算するだけです。
求める期待値は
(3×6+2×0+1×36+0×42)/84
=54/84
=9/14
となります。