東京慈恵会医科大学2025年数学第1問(解答・解説)
目の出方は全部で6×6×6=216通りあります。
(前半について)
さいころを3回ふる問題だから、6×6の表をかいて求めることもできますが、ここでは、表をかかずに求めることにします。
余事象を利用して解きます。
すべての場合の数は6×6×6=216通りあります。
このうち、出た目の積が10の倍数にならないのは、2の倍数(2、4、6)が1回も出ないか5の倍数(5)が1回も出ない場合になります。
出た目の積が10の倍数にならない場合は
3×3×3+5×5×5−2×2×2 ←2の倍数が1回も出ないというのは、3回とも奇数の目が出るということで、5の倍数が1回も出ないというのは、3回とも1、2、3、4、6のいずれかの目が出るということです。この2つの場合にはダブりがある(3回とも1か3の目が出る場合)ので、ダブりを取り除く必要があります。わかりにくければヴェン図をかくとよいでしょう。
=27+125−8
=144通り
あるから、出た目の積が10の倍数になる場合は
216−144
=72通り
あり、求める確率は72/216=1/3となります。
東大や京大でも同じような問題(京都大学1992年前期理系数学第4問・文系数学第4問、東京大学2003年前期理科数学第5問、京都大学2023年理系数学第3問など)が出されているので、ぜひ解いてみましょう。
(後半について)
どの2回の出た目の和も6の倍数(6か12)とならない確率を求めるということですね。
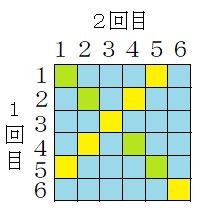
どの2回の出た目の和も6の倍数(6か12)とならない場合を6×6の表を用いて数え上げます。
1回目と2回目の時点での表をかき、3回目に出た目については、表の各マス目にブロックを積むイメージで考えます。
図の黄色の部分の6マスについては、さいころを2回振った時点で条件を満たさないことが確定していますね。
図の黄緑色の部分の4マス(2回振った時点では条件を満たしているもののうち2つの目が同じ場合)については、3回目は1つの目以外条件を満たします。 ←1(2)回目の出た目が1、2、4、5の場合に条件を満たさないのは、3回目の出た目がそれぞれ5、4、2、1の場合となります。実際には、具体的にすべてをチェックする必要はなく、1(2)回目に出た目との和が6になるものだけが排除されるだけのことです。
この場合は、5×4=20通りあります。
図の水色の部分の36−6−4=26マス(2回振った時点では条件を満たしているもののうち2つの目が異なる場合)については、3回目は2つの目以外条件を満たします。 ←1回目に出た目との和が6(ただし、1回目に出た目が6のときは12)になるものと2回目に出た目との和が6(ただし、2回目に出た目が6のときは12)になるものだけが排除されます。
この場合は、4×26=104通りあります。
したがって、求める確率は
(20+104)/216
=31/54
となります。