九州大学2025年前期理系数学第3問・文系数学第3問(解答・解説)
(1)
整数nを4で割ったときの商を△、余りを○(○=0、1、2、3)とします。
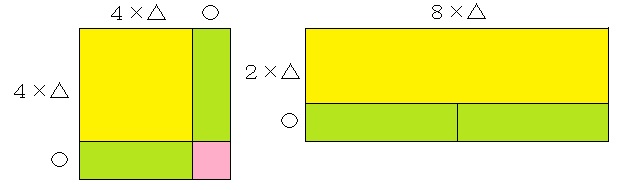
n2の面積図をかくと、次のようになります。 ←2数の積があれば、長方形(正方形)の面積に帰着させることができますね。
黄色の部分と黄緑色の部分を合わせたものは8で割り切れる(上の右側の図を参照)ので、n2を8で割ったときの余りは、ピンク色の部分(○×○)を8で割った余りと等しいことがわかります。 ←一般に、○を△で割ったときの余りが☆、□を△で割ったときの余りが★のとき、○×□を△で割ったときの余りは☆×★を△で割ったときの余りと等しくなります(和、差についても同様です)。上と同様の面積図をかけばすぐにわかります。
結局、n2を8で割ったときの余りは、0×0=0、1×1=1、2×2=4、3×3=9を8で割ったときの余りを考えればよく、0、1、4のいずれかとなります。
なお、高校生であれば、文字式を使って機械的に処理するだけの話です。
(2)
nは0以上の整数だから、n2+3は3以上となり、mは2以上となります。 ←下限チェック!
(1)より、n2+3を8で割った余りは0+3=3、1+3=4、4+3=7となり、8で割り切れることはありません。
mが3以上のとき、2mは8で割り切れるから、mは2以下となります。 ←上限チェック!
結局、条件を満たす可能性があるmは2だけとなります。
m=2のとき、4=n2+3で、nは0以上の整数だから、n=1となります。
したがって、答えは(2,1)となります。