摨巙幮拞妛峑侽侾擭戞俉栤乮夝摎丒夝愢乯
仛憡帡偵偮偄偰仛
俀偮偺恾宍偑憡帡偺応崌丄懳墳偡傞妏偑摍偟偔丄懳墳偡傞曈偺斾偑堦掕偱摍偟偔側傝傑偡丅
偝偰丄栤戣傪夝偄偰偄偒傑偟傚偆丅
栤戣偺恾宍偼丄俙俠偺拞揰偵娭偟偰懳徧乮揰懳徧恾宍乯偩偐傜丄偲傝偁偊偢壓敿暘乮嶰妏宍俙俛俠偺晹暘乯偩偗峫偊傑偡丅丂懳徧惈傪棙梡偟偰嶌嬈傪尭傜偡両
恾偺傛偆偵丄俙偲俠丄俤偲俥傪寢傃傑偡丅
嶰妏宍俙俛俠偲嶰妏宍俤俛俥偼憡帡乮憡帡斾偼丄俙俛丗俤俛亖俀丗侾乯偩偐傜丄俙俠丗俤俥亖俀丗侾偲側傝傑偡丅
嶰妏宍俬俤俥偺柺愊傪嘆偲偡傞偲丄嶰妏宍俬俠俙乮幬慄晹暘偺敿暘乯偺柺愊偼嘋丄嶰妏宍俬俥俠偺柺愊偲嶰妏宍俬俙俤偺柺愊偼嘇偲側傝傑偡丅丂仼乮戜宍傪俀杮偺懳妏慄偱暘妱偟偰偱偒傞嶰妏宍偺柺愊斾乯傪嶲徠偟傑偟傚偆丅
嶰妏宍俙俛俠偲嶰妏宍俤俛俥偼憡帡乮憡帡斾偼丄俙俛丗俤俛亖俀丗侾乯偩偐傜丄柺愊斾偼俀亊俀丗侾亊侾亖係丗侾偲側傞偺偱丄嶰妏宍俙俛俠偺柺愊偼
丂丂戜宍俤俥俠俙偺柺愊亊係/乮係亅侾乯
丂亖乮嘆亄嘋亄嘇亄嘇乯亊係/俁
丂亖嘖
偲側傝傑偡丅
寢嬊丄幬慄晹暘偺柺愊乮嘋亊俀乯偼丄暯峴巐曈宍俙俛俠俢偺柺愊乮嘖亊俀乯偺乮嘋亊俀乯/乮嘖亊俀乯亖侾/俁攞偲側傞偺偱丄
丂丂侾俀俇亊侾/俁亖係俀cm2
偲側傝傑偡丅
乮戜宍傪俀杮偺懳妏慄偱暘妱偟偰偱偒傞係偮偺嶰妏宍偺柺愊斾乯
忋掙偑a丄壓掙偑倐偺戜宍傪俀杮偺懳妏慄偱暘妱偟偰偱偒傞係偮偺嶰妏宍偺柺愊斾偼丄嵍忋恾偺傛偆偵側傝傑偡丅
塃忋恾偺墿椢怓偺嶰妏宍偲愒怓偺嶰妏宍偼憡帡乮憡帡斾偼丄忋掙丗壓掙亖a丗倐乯偩偐傜丄柺愊斾偼丄a亊a丗b亊b偲側傝傑偡丅
嵍忋恾偺墿椢怓偺嶰妏宍偲愒怓偺嶰妏宍偼憡帡乮憡帡斾偼丄忋掙丗壓掙亖a丗倐乯偩偐傜丄嵍忋恾偺傛偆側曈偺斾偵側傝傑偡丅偡傞偲丄塃忋恾偺巼怓偺幬慄晹暘偺柺愊偲惵怓偺幬慄晹暘偺柺愊偺斾偼a丗倐偲側傝傑偡丅丂仼崅偝嫟捠佀嶰妏宍偺柺愊斾亖掙曈偺斾
寢嬊丄惵怓偺幬慄晹暘偺柺愊偼丄巼怓偺幬慄晹暘偺柺愊偺b/a攞偲側傝傑偡丅
嵍忋恾偺悈怓偺嶰妏宍偺柺愊偲巼怓偺嶰妏宍偺柺愊偼摍偟偔側傝傑偡丅丂仼崅偝偲掙曈偑嫟捠偩偐傜丅
偦傟偧傟偺嶰妏宍偐傜嫟捠晹暘傪庢傝彍偄偨柺愊傕摍偟偔側傞偺偱丄塃忋恾偺惵幬慄晹暘偺嶰妏宍偺柺愊偼摍偟偔側傝傑偡丅
乮暿夝乯
暯峴巐曈宍俙俥俠俫偺柺愊偼丄暯峴巐曈宍俙俛俠俢偺柺愊偺侾/俀偲側傝傑偡丅丂仼乮暯峴慄偲柺愊斾乯傪嶲徠
恾偺傛偆偵丄俤俠偲暯峴側曗彆慄俬俥傪堷偒傑偡丅
偡傞偲丄嶰妏宍俛俥俬偲嶰妏宍俛俠俤偼憡帡乮憡帡斾偼丄俛俥丗俛俠亖侾丗俀乯偲側傞偺偱丄俛俬丗俛俤亖侾丗俀偲側傝傑偡丅俛俬亖嘆偲偡傞偲丄俬俤亖嘆丄俙俤乮亖俛俤乯亖嘇偲側傝傑偡丅
傑偨丄嶰妏宍俙俤俰偲嶰妏宍俙俬俥偼憡帡乮憡帡斾偼丄俙俤丗俙俬亖嘇丗乮嘇亄嘆乯亖俀丗俁乯偩偐傜丄俙俰丗俙俥亖俀丗俁偲側傝傑偡丅
摨條偵丄俠俲丗俠俫亖俀丗俁偲側傝傑偡丅丂仼懳徧惈乮揰懳徧乯傪峫椂両
傛偭偰丄暯峴巐曈宍俙俰俠俲偺柺愊偼丄暯峴巐曈宍俙俥俠俫偺柺愊偺俀/俁偲側傝傑偡丅丂仼乮暯峴慄偲柺愊斾乯傪嶲徠
埲忋傛傝丄媮傔傞柺愊偼丄暯峴巐曈宍俙俛俠俢偺柺愊乮侾俀俇cm2乯偺侾/俀亊俀/俁亖侾/俁攞丄偮傑傝丄
丂丂侾俀俇亊侾/俁亖係俀cm2
偲側傝傑偡丅
側偍丄儊僱儔僂僗偺掕棟傪抦偭偰偄傟偽丄俙俰丗俰俥亖俀丗侾傪娙扨偵弌偡偙偲偑偱偒傑偡丅
乮暯峴慄偲柺愊斾乯
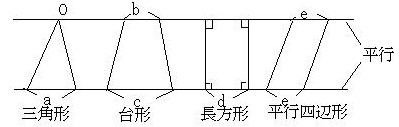
壓偺恾偺柺愊斾偼丄偄偢傟傕乽忋掙亄壓掙乿偺斾偱張棟偱偒傑偡乮挿曽宍傕暯峴巐曈宍傕戜宍偩偐傜丄嵍偺俀偮偱偡傋偰張棟偱偒傑偡丅傑偨丄嶰妏宍傪忋掙侽偺戜宍偲峫偊傞偲丄偡傋偰傪戜宍偲偟偰張棟偱偒傑偡偹乯丅
柺愊斾偼
丂丂乮侽亄a乯丗乮倐亄們乯丗乮倓亄倓乯丗乮e亄e乯
偲側傝傑偡丅