摨巙幮拞妛峑俀侽侾俇擭嶼悢戞俈栤乮夝摎丒夝愢乯
偲傝偁偊偢桿摫傪柍帇偟偰儊僀儞偺乮俀乯傪夝偒傑偡丅
侾墲暅偱峫偊傑偡丅
侾墲暅偺帪娫偼俆帪娫係侽暘亄俆帪娫亖侾侽帪娫係侽暘亖亖俇係侽暘偱偡偹丅
丂懍偝偺斾丂忋傝丗壓傝亖俁丗俆
丂丂伀媡斾仼嫍棧堦掕乮俙俛娫偺嫍棧乯
丂帪娫偺斾丂忋傝丗壓傝亖俆丗俁亖嘍丗嘊
嘍亄嘊亖嘒偑俇係侽暘偵憡摉偡傞偐傜丄壓傝偵偐偐偭偨帪娫乮嘊乯偼俇係侽亊嘊/嘒亖俀係侽暘亖係帪娫偲側傝傑偡丅
偟偨偑偭偰丄俙挰偐傜俛挰傑偱偺摴偺傝偼俆亊係亖俀侽km偲側傝傑偡丅
側偍丄斾偱張棟偟偨晹暘偼師偺傛偆偵偡傞偙偲傕偱偒傑偡丅
侾俆km偺嫍棧傪忋傝壓傝偡傞偲丄侾俆/俁亄侾俆/俆亖俉帪娫亖係俉侽暘偐偐傞偐傜丄俇係侽暘忋傝壓傝偡傞偲丄侾俆亊俇係侽/係俉侽亖俀侽km忋傝壓傝偟偨偙偲偵側傝丄偙傟偑摎偊偲側傝傑偡丅
偙偙偐傜丄幹懌偺乮侾乯偲偍晅偒崌偄偟側偄偲偄偗傑偣傫丅
懍偝偺偮傞偐傔嶼偵傛傝丄俛摶娫偺忋傝偵偐偐偭偨帪娫偼乮俆亊俆亅俀侽乯/乮俆亅俁乯亖俆/俀帪娫偲側傝丄媮傔傞摴偺傝偺嵎偼俀侽亅俁亊俆/俀亊俀亖俆km偲側傝傑偡丅
偙傟偑嵟抁偺夝朄偵側傝傑偡偑丄弌戣幰偺桿摫乮摶偲懍偝偺栤戣偵傛偔偁傞桿摫乯偵廬偭偰夝偔偲師偺傛偆偵側傝傑偡丅
乮侾乯
俙偐傜俛偵峴偔偲偒偺傎偆偑俛偐傜俙偵峴偔偲偒傛傝帪娫偑偐偐偭偰偄傞偺偱丄俙偐傜摶傑偱偺摴偺傝偺傎偆偑俛偐傜摶傑偱偺摴偺傝傛傝挿偄偱偡偹丅
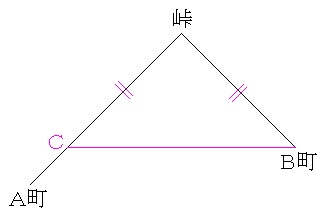
偦偺摴偺傝偺嵎偺晹暘乮恾偺俙俠娫乯乯偵拝栚偟傑偡丅
丂懍偝偺斾丂忋傝丗壓傝亖俁丗俆
丂丂伀媡斾仼嫍棧堦掕乮俙俠娫乯
丂帪娫偺斾丂忋傝丗壓傝亖俆丗俁亖[俆]丗[俁]
[俆]亅[俁]亖[俀]偑俆帪娫係侽暘亅俆帪娫亖係侽暘偵憡摉偡傞偐傜丄俙俠娫偺壓傝偵偐偐偭偨帪娫乮[俁]乯偼係侽亊[俁]/[俀]亖俇侽暘亖侾帪娫偲側傝丄媮傔傞摴偺傝偺嵎偼俆亊侾亖俆km偲側傝傑偡丅
偙偙傑偱偺帪揰偱丄傗偭偰偄傞偙偲偼嵟弶偵弎傋偨夝朄偲傎傏摨偠偱偡偑丄儊僀儞偺栤戣偺夝寛偵偼帄偭偰偄傑偣傫丅
偙偺栤戣偵偍偄偰偼丄偙偪傜偺夝朄偺傎偆偑楎偭偰偄傞偙偲偑傛偔傢偐傝傑偡偹丅
乮俀乯
俛偐傜俠傑偱峴偔偲偙傠偱峫偊傑偡丅
丂懍偝偺斾丂忋傝丗壓傝亖俁丗俆
丂丂伀媡斾仼嫍棧堦掕乮俛摶娫乮亖摶俠娫乯乯
丂帪娫偺斾丂忋傝丗壓傝亖俆丗俁亖亙俆亜丗亙俁亜
亙俆亜亄亙俁亜亖亙俉亜偑俆帪娫乕侾帪娫亖係帪娫偵憡摉偡傞偐傜丄俛摶娫偺忋傝偵偐偐偭偨帪娫乮亙俆亜乯偼係亊亙俆亜/亙俉亜亖俆/俀帪娫偲側傝傑偡丅
偟偨偑偭偰丄俙挰偐傜俛挰傑偱偺摴偺傝偼
丂丂俁亊俆/俀亊俀亄俆
丂亖俀侽km
偲側傝傑偡丅