甲陽学院中学校2000年算数2日目第4問(解答・解説)
(1)
辺の比を求める問題です。
辺の比を求める問題では、面積比の利用または相似の利用が基本です。
この問題の場合、面積比はすぐに求まりそうにないから、相似を利用することになります。
与えられた条件(AB:BD=2:3)を求めるもの(BD:DF)に近づけていくようにするのがポイントですね。
C、E、Gが1直線上にあるんだから、C、E、Gを直線で結んでみましょう。
すると、相似な三角形が登場しますね。
3つの正三角形が相似なのは当たり前ですが、三角形BECと三角形DGEも相似になります。(2組の角がそれぞれ等しいから。)
三角形BECと三角形DGEの相似比は
BC:DE
=AB:BD 正三角形ABCとBDEの相似を利用しました。
=2:3
となります。
相似の場合、対応する辺の比が等しいから
BE:DG
=2:3
あとは、正三角形BDEと正三角形DFGの相似を利用すればいいでしょう。
相似の場合、対応する辺の比が等しいのだから
BD:DF
=2:3
(2)
だから、面積比は
三角形ABC:三角形BDE:三角形DFG
=4×4:6×6:9×9
=[16]:[36]:[81]
BCとDEが平行で、BC:DE=2:3だから
三角形BECの面積
=三角形BDEの面積×2/3 ←(平行線と面積比)を参照しましょう。
=[36]×2/3
=[24]
同様に、DEとFGが平行で、DE:FG=BD:DF=2:3だから
三角形DGEの面積
=三角形DFGの面積×2/3 ←(平行線と面積比)を参照しましょう。
=[81]×2/3
=[54]
となるので、
四角形AFGCの面積
=三角形ABCの面積+三角形BDEの面積+三角形DFGの面積+三角形BECの面積+三角形DGEの面積
=[16]+[36]+[81]+[24]+[54]
=[211]
[16]が1cm2に相当するから、四角形AFGCの面積は
1×[211]/ [16] 「和」+「比」で求める!!
=211/16cm2
なお、CGとAFを延長した線の交点Hを考えて解くこともできるでしょう。
(平行線と面積比)
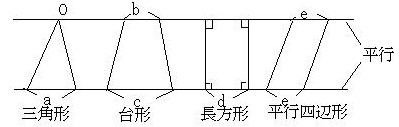
下の図の面積比は、いずれも「上底+下底」の比で処理できます(長方形も平行四辺形も台形だから、左の2つですべて処理できます。また、三角形を上底0の台形と考えると、すべてを台形として処理できますね)。
面積比は
(a+0):(b+c):(d+d):(e+e)
となります。