金蘭千里中学校2002年後期算数第4問(解答・解説)
(1)
直角三角形ABCは、右へ
16-12
=4cm
ずれているから、AD(=CF)の長さは
4cm
となります。
求める面積は
(4+16)×12×1/2 ←台形の面積公式を用いて直接求めましたが、直角二等辺三角形ABCの面積+長方形ACFDの面積とすることもできます(「和」(分割)で求める)。
=120cm2
となります。
(2)
四角形ABEDは平行四辺形ですね。
三角形ADGと四角形ABEGの面積の比が5:19だから、
GD:(AB+EG) ←(平行線と面積比)を参照しましょう。
=[5]:[19]
となり、AB(=ED)は
([5]+[19])÷2
=[12]
となります。
三角形ABCと三角形GDAは相似(ともに直角二等辺三角形)だから、
BC:DA
=AB:GD
=⑫:⑤
となります。
⑫が12cmに相当するから、ADの長さ(⑤に相当)は
12×⑤/⑫
=5cm
となります。
この問題では使いませんでしたが、平行四辺形ABEDの面積と長方形ACFDの面積は等しいから、共通部分の三角形AGDの面積を取り除いた部分の面積も等しくなる(台形ABEGの面積=台形CFDGの面積)こともぜひおさえておきましょう。
(平行線と面積比)
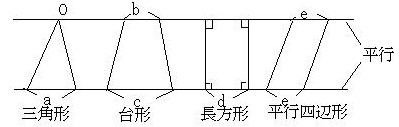
下の図の面積比は、いずれも「上底+下底」の比で処理できます(長方形も平行四辺形も台形だから、左の2つですべて処理できます。また、三角形を上底0の台形と考えると、すべてを台形として処理できますね)。
面積比は
(0+a):(b+c):(d+d):(e+e)
となります。