神戸女学院中学部2018年算数第5問(解答・解説)
(1)
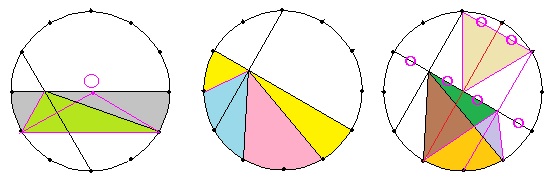
まず、上側にある部分を直径に関して折り返し、下側に移動させます。
斜線部分(灰色の部分)の面積
=灰色の部分の面積+黄緑色の部分の面積-黄緑色の三角形の面積
=円の1/12の面積×2+ピンク色の三角形の面積-黄緑色の三角形の面積 ←Oは円の中心です。
=円の1/6の面積 ←等積変形により、三角形の面積同士がうまく打ち消されますね。最初から、このことを見切っているから、このように解いています。
=9×9×3.14×1/6
=13.5×3.14
=31.4
9.42
+ 1.57
42.39cm2
(2)
(1)を利用します。
水色の部分とピンク色の部分の面積の和は、半円の面積から、黄色の部分の面積((1)で求めた面積ですね)を引いたものだから、円の1/2-1/6=1/3の面積、つまり、(1)で求めた面積の2倍(84.78cm2)となります。
水色の部分とピンク色の部分の面積の差を求めることを考えます。 ←和差算に持ち込みます。
水色の部分とピンク色の部分の面積の差を考えるので、(なるべく)重ね合わせることを考えます。
そこで、図の赤色の直径に関して水色の部分を折り返します。
ピンク色の部分の面積-水色の部分の面積
=(オレンジ色の部分の面積+茶色の部分の面積)-(オレンジ色の部分の面積+紫色の部分の面積)
=茶色の部分の面積-紫色の部分の面積 ←共通部分を取り除きました(差は変わりませんね)。
=(茶色の部分の面積+緑色の部分の面積)-(紫色の部分の面積+緑色の部分の面積) ←共通部分をつけたしました(差は変わりませんね)。
=9×9/2×1/2 ←図のクリーム色の正三角形の半分の三角定規に着目すると、図の〇をつけた長さは等しくなります。(茶色の部分の面積+緑色の部分の面積)は、底辺が〇2個分、高さが〇2個分の三角形で、(紫色の部分の面積+緑色の部分の面積)は、底辺が〇2個分、高さが〇1個分の三角形だから、その差は、底辺が〇2個分、高さが〇1個分の三角形の面積と一致します。
=20.25cm2
となります。
和差算により、求める面積(ピンク色の部分の面積)は
(84.78+20.25)/2
=105.03/2
=52.515cm2
となります。