神戸女学院中学部2023年算数第6問(解答・解説)
(1)
線対称性を利用して4等分した図で考えて解く解法(灘中学校2013年算数1日目第9問の解答・解説を参照)など様々な解法が考えられますが、ここでは、正方形ABCDの面積から4個の合同な直角三角形の面積を引いて斜めの正方形の面積と求め、さらに4個の合同な直角三角形の面積を引いて求めるという方針で解きます。
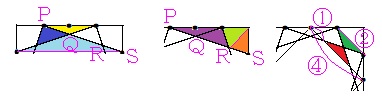
黄色の三角形と水色の三角形のちょうちょ相似(相似比は2:4=1:2)より、PQ:QS=1:2となります(条件の対等性により、斜めの正方形の他の部分についても同様)。
正方形が対角線について対称であることから、オレンジ色の三角形と黄緑色の三角形は合同で面積が等しく、また、「高さが等しい三角形の面積比は底辺の比と一致する」(以下(*)とする)から、紫色の三角形の面積は黄緑色の三角形の面積の2倍となります。
このことと(*)より、PR:RS=3:1となります(条件の対等性により、斜めの正方形の他の部分についても同様)。
斜めの正方形の面積は、水平な正方形の面積の
(4×4-3×1×1/2×4)/(4×4) ←「方眼紙」で求める!
=10/16
となります。
また、青色の三角形の面積は、斜めの正方形の面積の
1/2×1/(1+2)×1/(1+3) ←斜めの正方形の面積の半分の直角二等辺三角形の面積と比べました(いわゆる隣辺比)。その際、先ほど求めた比を利用しました。
=1/24
したがって、求める面積は
16×16×10/16×(1-1/24×4) ←「差」+「比」で求める!
=400/3cm2
となります。
(2)
線対称に着目し、(1)で求めた面積から図の赤色の三角形の面積4個を取り除くという方針で解きます。 ←「差」で求める!
2組のピラミッド相似に着目して辺の比を書き込むと図のようになり、正方形の対角線に関する対称性を利用すると、赤色の三角形と緑色の三角形のちょうちょ相似の相似比が(④-①×2):②=1:1となる(合同である)ことがかります。
緑色の三角形の面積は、(1)で求めた面積比と辺の比と(*)より、
(16×3/4)×(16×1/4)×1/2×2/(1+2)×1/(1+3)
=4cm2
となります。
したがって、求める面積は
400/3-4×4
=352/3cm2
となります。