神戸女学院中学部2024年算数第2問(解答・解説)
(1)
仕入れ単価の比 A:B=100:(100−20)=5:4=[5]:[4]
仕入れ個数の比 A:B=100:(100+20)=5:6
Aから5個、Bから6個仕入れようが、Aから10個、Bから12個仕入れようが、平均は変わらないので、Aから5個、Bから6個仕入れたと考えます。 ←このように考えずに[5]と[4]を5:6の比で混ぜ合わせると考えて天秤(てんびん)で処理してもよいでしょう。
平均仕入れ単価は
([5]×5+[4]×6)/(5+6)
=[49/11]
円となり、これが490円に相当するから、Bからの仕入れ単価は
490×[4]÷[49/11]
=440円
となります。
(2)
Aからの仕入れ単価は
440×[5]/[4]
=550円
となり、Cからの仕入れ単価は
440+440×30/100
=572円
となります。
3社からの仕入れ単価がAからの仕入れ単価と等しくなる場合を考えることになりますが、この場合、3社からAを除いた2社からの仕入れ単価がAからの仕入れ単価と等しくなります。
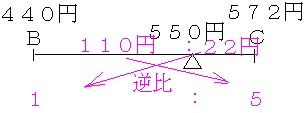
結局、Bからの仕入れ単価とCからの仕入れ単価の平均がAからの仕入れ単価になるということだから、天秤で処理します。 ←このことを見抜くことがポイントです。
Cからの仕入れ個数はBからの仕入れ個数の5倍となり、Aからの仕入れ個数の6/5×5=6倍となり、これが答えとなります。