神戸海星女子学院中学校2020年A算数第4問(解答・解説)
(1)
3つの目の和は1×3=3以上6×3=18以下で、12は上限値に近いので、大きい順に書き出していきます。
6−5−1
−4−2
5−4−3
したがって、答えは(1,5,6)、(2,4,6)、(3,4,5)となります。
(2)
30=2×3×5だから、3つのさいころの出た目の組み合わせは1、5、6か2、3、5となります。
いずれの場合もどのさいころがどの目になるかで3×2×1=6通りあるから、求める組は全部で6×2=12個あります。
(3)
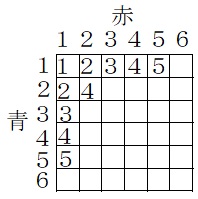
赤と青の2個のさいころの目の積を6×6の表で書き出すと次のようになります。
条件を満たすためには、目の積が5以下である必要があるので、目の積が5以下のところだけ書き出します。
目の積が1のところは、黄のさいころの目が1〜6の6通りあるから6倍し、目の積が2のところは、黄のさいころの目が2〜6の5通りあるから5倍し、・・・、目の積が5のところは、黄のさいころの目が6の1通りあるから1倍すればいいですね。
したがって、求める組は全部で1×5+2×4+2×3+3×2+2×1=27個あります。