慶應義塾中等部2022年算数第6問(解答・解説)
(1)
1から30(5×6)までの30個の数字を並べます。
123456
789101112
131415161718
192021222324
252627282930
右端の数は6の倍数だからすべて作ることができますね。
次に、5の倍数にピンク色を塗ります。 ←横に6個ずつ数字を並べているので、左斜め下方向に現れます。
ピンク色の下の数字は6を順次足していくことにより、すべて作ることができます。
残った数字を作ることはできないから、答えは19となります。 ←実際には、5×6−(5+6)とすぐに求められます。
(2)
11と13をまず1つずつ加え、それ以外の部分について考えます。 ←厳しい条件についてまず考えます。
これで(1)と同様の問題になりましたね。
1から143(11×13)までの143個の数字を並べます(もちろん、実際には数字を並べませんが・・・)。
右端は13の倍数だから、すべて作ることができますね。
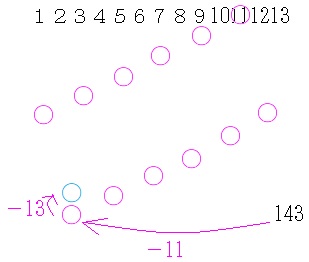
次に、11の倍数がある場所をチェックしていきます(図のピンクの〇)。 ←左斜め下方向に桂馬と同じ動きで現れます。ただし、上から6段目には左端とそこから右に11個移動したところの合計2個現れることに注意が必要です。
ピンクの〇の下の数字は13を順次足していくことにより、すべて作ることができます。
残った数字を作ることはできないから、作ることができない最大の整数(図の水色の〇)は、11×13−(11+13)となります。
したがって、答えは11+13+11×13−(11+13)=143となります。