慶應義塾普通部2019年算数第6問(解答・解説)
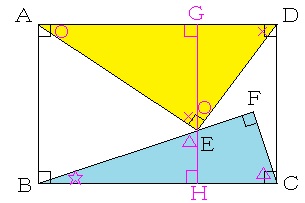
図のように、点Eを通り、辺ABに平行な直線GHを引きます。 ←この1本の補助線で2種類の直角三角形の相似が現れますね。(1)の誘導とメインの(2)から判断すると、この補助線を引くことが普通部の出題者の意図でしょうね。
直角三角形がたくさん登場するので、角度に記号をつけ、辺の比をチェックすると、3辺の辺の比が45:60:75=3:4:5の相似な直角三角形(黄色の部分)と3辺の辺の比が21:72:75=7:24:25の相似な直角三角形(水色の部分)があることが分かりますね。
(1)
EGの長さを求めればいいですね。
EGの長さは
AEの長さ×3/5
=60×3/5
=36cm
となります。
(2)
BHの長さ、言い換えれば、AGの長さは
AEの長さ×4/5
=60×4/5
=48cm
だから、EHの長さは
BHの長さ×7/24
=48×7/24
=14cm
となります。
したがって、ABの長さ、言い換えれば、GHの長さは、
36+14
=50cm
となります。