慶應義塾普通部2021年算数第2問(解答・解説)
①
求める角の大きさは、正五角形と正八角形の外角の差となるから、
360/5-360/8
=72-45
=27度
となります。
②
ちまちまと角度を求めていっても解けますが、ここでは暗算でさっと解く解法を紹介します。
文章にすると長々しいですが、実際には暗算で答えが求められます。
以下、矢印の長さを適宜変えています。
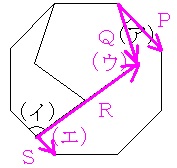
矢印Pを(ア)の角の大きさだけ時計回りに回転すると矢印Qになり、矢印Qを(ウ)の角の大きさ(180-72=108度)だけ反時計回りに回転すると矢印Rになり、矢印Rを(エ)の角の大きさだけ時計回りに回転すると矢印Sになります。
結局、矢印Pが1回転することなく同じ方向の矢印Sとなっているから、時計回りの角の大きさの合計と反時計回りの角の大きさの合計が等しくなります。
したがって、(エ)の角の大きさは
108-27
=81度
となり、(イ)の角の大きさは
180-81
=99度
となります。