灘高等学校2024年数学第1問(3)(解答・解説)
図が与えられていないので、自分で図をかく必要があります。
その際、いきなり正確な図をかこうとするのではなく、とりあえず適当な図をかいて(思い浮かべて)、その後、それなりに正確な図をかくことが大切です。
なお、問題文を真に受けて三角形ABCを折り返した図をかいてはいけません。
2点D、Fを直線で結びます。
線対称性より、三角形DGAと三角形DGFは合同となり、AD=FDとなります。
図のような直線FHを引き、二等辺三角形BFDを線対称の軸で2つの合同な直角三角形に分けると、三角形ABCと三角形FHBは相似となります。 ←角度に記号をつければわかることです。
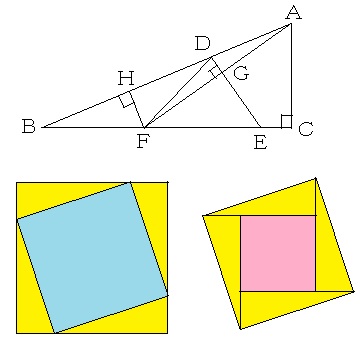
ここで、ABの長さを求めるために、直角三角形ABC(黄色の三角形)を4個並べることにより、正方形を作り出します。 ←合同な直角三角形を4個並べることにより正方形を作出することは、斜めの正方形がらみの問題や直角三角形の斜辺(直角の向かいの辺)を求める際などの必須手法です。
左側の図において、水色の正方形の面積は(5+12)×(5+12)−5×12×1/2×4=289−120=169=13×13となるから、ABの長さは13cmとなります。 ←それなりのレベルの中学校の受験生であれば、5:12:13の直角三角形の知識から直ちに求めることができるでしょう。
なお、右側の図で、5×12×1/2×4+(12−5)×(12−5)=120+49=169=13×13としてもよいでしょう。
AD=BF=[13]とすると、BH=DH=[12]となり、[12]×2+[13]=[37]が13に相当するから、BFの長さは13×[13]/[37]=169/37となります。