大阪星光学院高等学校2023年数学第3問(解答・解説)
約束記号の問題なので、ルールに従って計算していくだけです。
3の倍数判定法(ある整数を3で割った余り=その整数の各位の和を3で割った余り)と「一般に、□で割った余りが〇の数と△の数の積を□で割った余りは、〇×△を□で割った余りと一致する」(☆)ことを利用します。
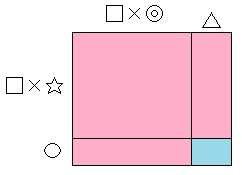
(☆)については下のような面積図を考えればすぐにわかります。
ピンク色の部分は□で割り切れるから、水色の部分を□で割った余りだけを考えればいいですね。
(1)
1024→1+0+2+4→1だから、f(1024)=1、f(1024×1025)=f(1×2)=f(2)=2となります。
(2)
1から2023までの整数を3で割った余りは1、2、0の3個の数の繰り返しとなります。
2023÷3=674・・・1だから、f(1)+f(2)+f(3)+・・・+f(2023)=(1+2+0)×674+1=2023となります。 ←1、2、0の3個の数の平均は1だから、全部1と考えることができ、また、2023を3で割った余りは3の倍数判定法により1となることがすぐにわかるので、実際には、割り算をするまでもなく答えが2023とわかります。
(3)
2023、71を3で割った余りはそれぞれ1、2となりますね。
f(20232)=f(1×1)=f(1)=1、f(712)=f(2×2)=f(4)=1だから、f(f(20232)×f(71))+f(2023)×f(712)=f(1×2)+f(1)×f(1)=f(2)+f(1)×f(1)=2+1×1=3となります。