灘高等学校2020年数学第3問(解答・解説)
(1)
3桁の整数が2の倍数となるのは、一の位の数が偶数(2か4か6)のときで、3桁の整数が5の倍数となるのは、一の位の数が5の倍数(5)のときで、同時に起こることはないので、3桁の整数が2の倍数または5の倍数となるのは、一の位の数が2か4か5か6のときになります。
3桁の整数は全部で6×6×6通りあり、そのうち条件を満たすものが4×6×6通りあるから、求める確率は(4×6×6)/(6×6×6)=2/3となります。
(2)
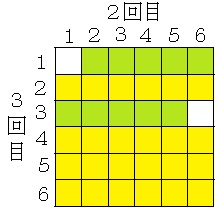
2回目と3回目に出た目の数で6×6の表を作成します。
図の黄色の部分(これが(1)で考えた部分になります)は4×6×6通りあります。
この部分に関しては9の倍数の条件を考えてはいけません。
ダブりが生じてしまいますから。
残りの部分(2でも5でも割り切れないとき)について9の倍数の条件を考えます。
各位の数の和が9の倍数となることをチェックすることになるので、2回目と3回目に出た目の数の和を書き込みます。 ←数が連番で並ぶだけなので、この作業は実際には省略できます。
さいころを3回ふったときの出た目の数の和は1×3=3以上6×3=18以下ですが、3回目に出た目の数が6の場合はもう考えてはいけないので、各位の数の和として考えらるもの9だけですね。
2回目と3回目に出た目の数の和が9−6=3以上9−1=8以下の場合(図の黄緑色の部分)だけ1通りずつ条件を満たす場合があります。
したがって、求める確率は
(4×6×6+10)/(6×6×6)
=77/108
となります。