慶應義塾高等学校2018年数学第3問(解答・解説)
(1)
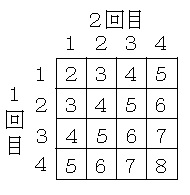
さいころを2回振る問題では6×6の表をかいて解きますが、この問題では4×4の表をかいてとけばよいでしょう。 ←Aが正四面体のサイコロを2回ふっているのと同じことですね。
Aの得点は次のようになります。
Aの取り出し方は全部で4×4=16通りあり、このうち、Aの得点が4未満つまり3以下となる場合は、1+2=3通りあるから、求める確率は(16−3)/16=13/16となります。
(2)
Bの得点がAの得点を上回る可能性があるのは、Aの得点が2点以上5点以下の場合だけですね。
Aの得点 Bの得点
2(1通り)・・・3〜6の4通り
3(2通り)・・・4〜6の3通り
4(3通り)・・・5、6の2通り
5(4通り)・・・6の1通り
2人の取り出し方は全部で16×6通りあり、そのうちBの得点がAの得点を上回る取り出し方は1×4+2×3+3×2+4×1=20通りあるから、求める確率は20/(16×6)=5/24となります。