灘高等学校2025年数学第1問(3)(解答・解説)
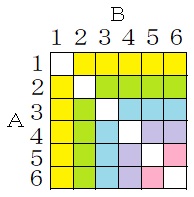
さいころを2個振る問題だから、6×6の表を書きます。 ←実際のところ、この程度の問題であれば、0点は6通り、1点は5×2=10通り、2点は4×2=8通り、3点は3×2=6通り、4点は2×2=4通り、5点は1×2=2通りとすぐに求められます(条件の対等性を利用して「×2」としています)が、一応表をかいておきます。
図の黄色、黄緑色、水色、紫色、ピンク色の部分の得点はそれぞれ1点、2点、3点、4点、5点となります。
実際には、条件の対等性を考慮し、左下半分だけで作業を行えばよいでしょう。 ←条件の対等性を利用して作業を減らす!
2回の得点の合計が5点となるのは、次の6パターンがあります。
(あ)0点・5点・・・6×2=12通り
(い)1点・4点・・・10×4=40通り
(う)2点・3点・・・8×6=48通り
(え)3点・2点 ←条件の対等性より(う)と同じですね(以下同じ)。
(お)4点・1点
(か)5点・0点
すべての場合は(6×6×6×6)通りだから、求める確率は
(12+40+48)×2/(6×6×6×6)
=25/162
となります。