開成中学校2023年算数第2問(解答・解説)
直線PQによって分けられた2つの部分のうち小さい方の面積は正六角形の面積の1/3となります。
大雑把に見当をつけると、条件を満たす1回目はQがCを過ぎたあたりだとわかりますね。 ←仮に、QがCの手前であっても修正すればいいだけですね。
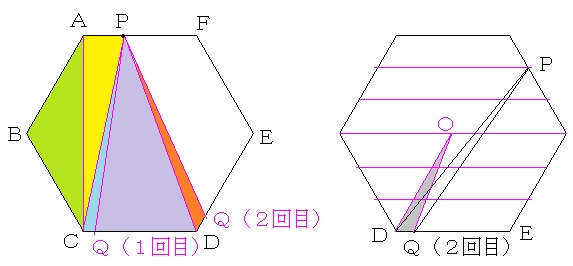
正六角形の6分割の知識(神戸女学院中学部2007年算数第5問の解答・解説を参照)を利用すると、黄色の部分の面積が正六角形の面積の1/3×1/3=1/9で、黄緑色の面積が正六角形の面積の1/6で、合計が正六角形の面積の1/9+1/6=5/18だから、あと1/3−5/18=1/18増やす必要があります。
結局、水色の部分の面積が正六角形の面積の1/18=1/3×1/6=三角形PCDの面積×1/6だから、CQの長さはCDの長さの1/6となります。 ←「三角形の高さ一定⇒底辺の比=面積の比」となることを利用しました。
したがって、条件を満たす1回目は(2+1/6)分後、つまり2分10秒後となります。
この1回目の状況から、直線PQの左側の面積を正六角形の面積の1/3だけ増やすことを考えます。 ←1回目を利用して2回目を求める際の作業を減らします。
紫色の面積が1/3×5/6だから、オレンジ色の面積は1/3×1/6=1/18となります。
このとき、仮にPが正六角形の中心Oにあったとすると、三角形ODQの面積は1/18×3/5=1/30=1/6×1/5=正三角形ODEの面積×1/5となり、DQの長さはDEの長さの1/5となります。 ←三角形PDQと三角形ODQの面積比を比べる際、等分割された線(図を参照)を思い浮かべ、「三角形の底辺一定⇒面積比=高さの比」を利用しました。また、DQとDEの長さを比べる際、「三角形の高さ一定⇒底辺の比=面積の比」となることを利用しました。
したがって、条件を満たす2回目は(3+1/5)分後、つまり3分12秒後となります。