灘中学校2014年算数2日目第3問(解答・解説)
問題文にある例を活用して解きます。
タイルの長さがすべて1/10になったと考えても同じだから、以下、タイルの長さがすべて1/10になったと考えて解きます。
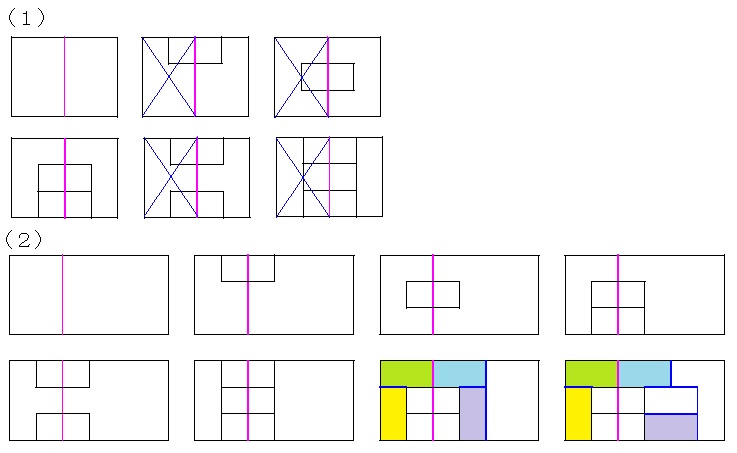
(1)
横のちょうど半分のところに縦線(図のピンク色の線)を引きます。
この線をまたぐタイルの個数で場合分けして考えます。
(あ)0個の場合
問題文の例より、ピンク色の線の左側も右側も3通りあるから、この場合は3×3=9通りあります。
(い)1個の場合
またぐタイルが上、中、下の場合がありますが、いずれの場合も左側をタイルでしきつめることができないので、この場合はありません。 ←下の場合は、上の場合の上下をひっくり返しただけなので、実際には考える必要はありません(対称性を利用して作業を減らす!)。なお、左がをタイルでしきつめることができないというのは、(2)においても決定的な役割を果たします。
(う)2個の場合
またがないタイルが上、中、下の場合があります。
上の場合は1通りあり、下の場合も同様に1通りあります。
中の場合は左側をタイルでしきつめることができないので、この場合はありません。
(え)3個の場合
左側をタイルでしきつめることができないので、この場合はありません。
(あ)〜(え)より、タイルのしきつめ方は全部で9+1×2=11通りあります。
(2)
横の左から2cmのところに縦線(図のピンク色の線)を引きます。
この線をまたぐタイルの個数で場合分けして考えます。
(あ)0個の場合
問題文の例と(1)より、ピンク色の線の左側は3通りあり、そのそれぞれに対して右側は11通りあるから、この場合は3×11=33通りあります。
(い)1個の場合
またぐタイルが上、中、下の場合がありますが、(1)の(い)同様、いずれの場合も左側をタイルでしきつめることができないので、この場合はありません。
(う)2個の場合
またがないタイルが上、中、下の場合があります。
上の場合について考えます。
左側からタイルを順にしきつめていくと、黄色、黄緑色、水色の部分は自動的に確定します。
次に、またいだ2個のタイルのすぐ右側の長方形のタイルを縦長にするか横長にするかで場合分けして考えます。
縦長にすると、残った部分は問題文の例のしきつめ方を考えればよく、3通りあります。
横長にすると、残った部分は自動的に確定し、1通りあります。
結局、上の場合は3+1=4通りあり、下の場合も同様に4通りあります。
中の場合は、(1)の(う)の中の場合同様、左側をタイルでしきつめることができないので、この場合はありません。
(え)3個の場合
(1)の(え)の場合同様、左側をタイルでしきつめることができないので、この場合はありません。
(あ)〜(え)より、タイルのしきつめ方は全部で33+4×2=41通りあります。