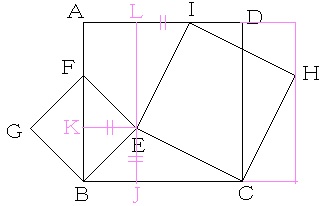
灘中学校2023年1日目第10問(解答・解説)
(解法1)
角FEIと角BECの和が180度で、EF=BEであることに着目して、三角形BCEをEを中心に時計回りに90度回転すると、面積が与えられている図形全体は、下の左端の図のようになります。 ←同様の手法については、東海中学校2006年第8問の解答・解説を参照しましょう。
上の真ん中の図のように、これを互い違いに4個組み合わせる(算数オリンピックや灘中入試ではよくある手法です)と、面積が(65+56)×4=121×4=22×22cm2の大きな正方形ができるから、その大きな正方形の一辺の長さ(〇+△)は22cmとなります。
また、この大きな正方形を上の右端の図のように分けると、小さな正方形の面積は121×4−56×8=9×4=6×6cm2となり、小さな正方形の一辺の長さ(〇−△)は6cmとなります。
和差算を解くと、△=(22−6)/2=8cmとなります。
正方形BEFGの対角線の長さは、△の半分の2倍、つまり、△と同じだから、求める面積は8×8×1/2=32cm2となります。
(解法2)
正方形の1辺が斜辺となっている直角三角形があるので、合同な直角三角形をつけたし、大きな正方形を作り出します。 ←同様の手法については、東海中学校2016年第8問の解答・解説を参照しましょう。
三角形BJEをEを中心に時計回りに90度回転し、等しい長さに着目すると、長方形AKELの面積は三角形EJC(三角形ILE)の面積の2倍であることが分かります。
結局、三角形EJCの面積の4倍が56cm2となるから、正方形ABCD(辺LJを一辺とする正方形と合同)の面積は65+56=121=11×11cm2となり、辺AB(AK+KB)の長さは11cmとなります。
ここから、(解法1)で示した正方形の分割に持ち込むこともできますが、ここでは違う手法で解きます。
長方形AKELの面積が56/2=28cm2となるから、AKとKE(KB)の積が28となります。
和が11、積が28となる2数は4と7だから、KBの長さは4cmとなり、求める面積は(4×2)×(4×2)×1/2=32cm2となります。