灘中学校2024年算数1日目第8問(解答・解説)
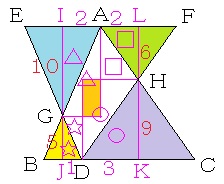
与えられた条件から、図の色をつけた三角形はすべて二等辺三角形となります。
二等辺三角形を線対称の軸で二等分するために、補助線IJ、KLを引くと、四角形IJKLは長方形となります。
JDの長さを1とすると、与えられた条件より、DK、IA、ALの長さはそれぞれ3、2、2となります。
三角形GJDと三角形GIEは相似(相似比はJD:IE=1:2)だから、JG:IG=1:2(=5:10)となります。
また、三角形HKDと三角形HLFは相似(相似比はDK:FL=3:2)だから、HK:HL=3:2(=9:6)となります。
結局、図のように長さをおくことができます。 ←長さを決めつけても面積比は変わりませんね。
図のように、長方形IJKLを分割する(オレンジ色の長方形の部分は重なります)と、同じ記号をつけた三角形はそれぞれ合同になり、面積も等しくなります。 ←過去に算数オリンピックや灘中学校で同種の問題が出されたことがあります(灘中学校2008年算数1日目第8問)。
オレンジ色の長方形の縦の長さは10−6=4で、横の長さは2−1=1だから、四角形AGDHの面積は
(長方形IJKLの面積−オレンジ色の長方形の面積)×1/2
=(15×4−4×1)/2
=28
となります。
三角形AHFの面積(□2個分の面積)は6×2=12となるから、四角形AGDHの面積は三角形AHFの面積の28/12=7/3倍となります。