灘中学校2025年算数2日目第4問(解答・解説)
同一平面上の2点がないので、立体の影の問題を処理する際の解法(真上から見た図で処理する解法)で切り口をあぶりだすことにします。
アルファベットの横の( )の中の数字は下からの高さを表すものとします。
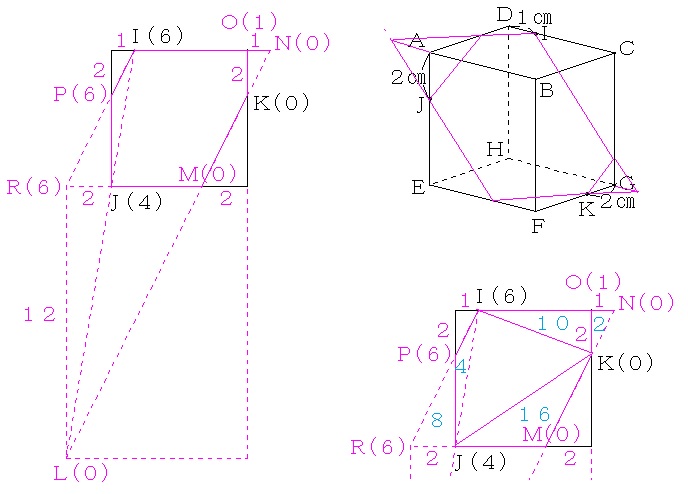
IJを直線で結び、下の面と交わった点をLとします。
IからJまで移動する間に高さが2下がり、左に1、前に6移動しているから、JからLへ高さが4下がる間に、左に2、前に12移動することになります。
LとKを直線で結び、直線EF、GHと交わった点をそれぞれM、Nとします。
LからKまで右に2+6=8移動する間に、後ろに12+4=16移動しているから、MからKまで後ろに4移動する間に、右に2移動することになり、KからNまで後ろに2移動する間に、右に1移動することになります。
ここで平行な面にできる切り口の線は平行であることを利用すると、上の面の切り口の線もわかりますね。
図の直線IPRは直線MKNと並行で、長さが等しくなりますね。
NとIを直線で結び、直線CGと交わった点をOとします。
NからIまで、左に6移動する間に、上に6移動しているから、NからOまで左に1移動する間に、上に1移動することになります。
言葉でかくと面倒そうですが、実際には比例を使っただけの単純作業です。
これで問題を解く準備ができました。
(1)
上の左側の図だけで立体の図をイメージして解くこともできますが、立体をイメージできない人は、上の右側のような立体の図を復元すればよいでしょう。
図の立方体の左側に2cm分の直方体があると考えて、高さ平均を利用して解くことにします。
求める体積は
6×6×{0+(2+6+1)}/2−(6×6×2−2×4×1/2×2×1/3)−1×2×1/2×1×1/3
=6×6×9/2−6×6×2+8/3−1/3 ←ひきすぎたら、たす!
=6×6×5/2+7/3
=92・1/3cm3 ←92・1/3というのは、92と1/3のことです。
となります。
(2)
立体の図を使わないほうがいいでしょう。
平行四辺形IRMNの面積を6×6×2=72と考えます。
いわゆる隣辺比と等しい高さの面積比を利用して、面積を書き込むと図の水色の数字のようになります。
切り口の面積は72−8−2=62となり、三角形IJKの面積は62−4−16−10=32となるから、切り口の面積は三角形IJKの面積の62/32=31/16倍となります。