灘中学校1993年算数1日目第12問(解答・解説)
右端の台形の上底と下底の長さの差は左端の三角形の「上底と下底の長さの差」、つまり、底辺の長さに他なりません。 ←右端の台形の上底と左端の三角形の「上底」の和と、右端の台形の下底と左端の三角形の「下底」の和は等しいですね。右の図を見るとわかりやすいでしょう。
このことに気づけば、10秒程度で解けます。
あとは、平行線と面積比に関する知識を利用するだけです。
右端の台形の上底と下底の長さの差(左端の三角形の底辺の長さ)は
8×2×21/(21+15+24)
=28/5(=5.6)cm
となります。
なお、この問題の場合、平行線と面積比に関する知識を利用せずに、平行四辺形の高さ(左端の三角形の高さでもありますね)を、平行四辺形の面積の逆算で求めた後、左端の三角形の面積の逆算を利用して、左端の三角形の底辺の長さを求めることもできます。
(平行線と面積比)
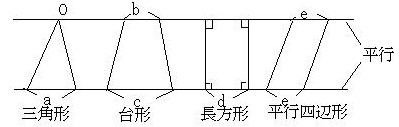
下の図の面積比は、いずれも「上底+下底」の比で処理できます(長方形も平行四辺形も台形だから、左の2つですべて処理できます。また、三角形を上底0の台形と考えると、すべてを台形として処理できますね)。
面積比は
(0+a):(b+c):(d+d):(e+e)
となります。