南山中学校女子部2023年算数第7問(解答・解説)
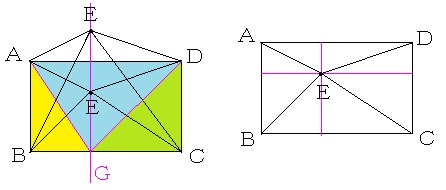
(1)、(2)において、三角形EABの面積と三角形ECDの面積の合計は長方形ABCDの面積の半分となります。
このことは図(下の左側の図)のように等積変形すればわかります。
点Eが、図1(図2)の点Eを通り、辺ABに平行な直線上のどこにあっても、三角形EABの面積は三角形GABの面積は等しくなり、三角形ECDの面積は三角形GCDの面積と等しくなります。
また、三角形GADの面積は長方形ABCDの面積の半分となるから、最初に述べたことが成り立ちます。
(1)
図1の三角形EBCの面積は
三角形EABの面積+三角形ECDの面積−三角形EDAの面積
=64+128−48 ←最初に述べたことから、三角形EDAの面積と三角形EBCの面積の合計は、長方形ABCDの面積の半分となり、三角形EABの面積と三角形ECDの面積の合計と等しくなりますね。なお、上の右側の図を考えてもこのことがわかりますね。
=144cm2
となります。
(2)
図1の三角形EBCの面積は
長方形ABCDの面積+三角形EDAの面積−(三角形EABの面積+三角形ECDの面積)
=三角形EABの面積+三角形ECDの面積+三角形EADの面積 ←長方形ABCDの面積−(三角形EABの面積+三角形ECDの面積)は、三角形EABの面積+三角形ECDの面積にほかなりませんね。
=64+128+48
=240cm2
となります。
なお、図2の三角形EBCの面積は図1の三角形EBCの面積に三角形EADの面積の2倍を足したものになります。 ←なぜそうなるか自分で考えてみましょう。
このことに着目して解いてもいいでしょう。
因みに、(2)だけを解くのであれば、等積移動して解くこともできるの自分で考えてみましょう(ヒント:三角形EDAを真下に移動させます)。