南山中学校女子部2024年算数第12問(解答・解説)
問題文の図の15度という条件は不要(与えられた他の条件から求められます)なので、無視して解きます。
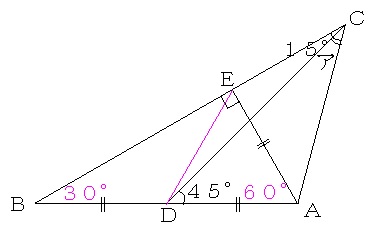
三角形ABEは、角Eが直角で、辺ABの長さが辺AEの長さの2倍だから、正三角形の半分の三角定規となり、残り2つの角の大きさが図のようになります。
三角形BDCにおいて、外角定理を利用すると、問題文の図の15度のところが45−30=15度というように求められます。
2点DとEを直線で結ぶと、三角形AEDは正三角形となり、DE=AEとなり、角EDC=60−45=15度となります。
三角形EDCは二等辺三角形となるから、DE=CEとなります。
したがって、CE=AEとなるから、三角形ACEは正方形の半分の三角定規(直角二等辺三角形)となり、角アの大きさは45−15=30度となります。