南山中学校女子部2024年算数第14問(解答・解説)
一般に、直角三角形の斜辺(直角の向かいの辺)の長さと残り2辺の長さの和か差が与えられると、直角三角形を並べて正方形を作り出すことにより、直角三角形の面積を求めることができます。
(1)のヒントでその誘導がなされていますが、誘導がなくても自分でできないといけません。
(1)
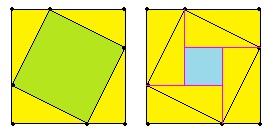
直角三角形ABC(黄色の三角形)を上の左側の図のように4個並べると、大きな正方形の一辺の長さ(ABの長さ+BCの長さ)は23cmとなり、小さな正方形(黄緑色の正方形)の一辺の長さは17cmとなります。
したがって、直角三角形ABCの面積は
(23×23−17×17)/4
=(23+17)×(23−17)/4 ←和と差の積=2乗の差(南山中学校女子部2024年算数第1問(4)の解答・解説を参照)を利用しました。
=10×6
=60cm2
となります。
(2)
上の左側の図に、直角三角形ABC(黄色の三角形)をさらに4個並べると、上の右側の図のようになります。
中心部の小さな正方形(水色の正方形)の面積は
17×17−60×4
=289−240
=49
=7×7cm2
となるから、水色の正方形の一辺の長さ(BCの長さ−ABの長さ)は7cmとなります。
和差算により、BCの長さは
(23+7)/2
=15cm
となります。