桜蔭中学校2018年算数第2問(2)(解答・解説)
図の同じ色を付けたところは条件的に同じとなります。 ←正六角形の中心を回転の中心として60度回転すると重なるからです。
①
同じ色をつけたところはどれを選んでも回転すると重なります。
結局、どの色を選ぶかだけを考えればよく、模様は4通りできます。
②
次の2つの場合が考えられます。
(あ)4色の色のうち同じ色のところから2か所選ぶ場合
(い)4色の色のうち異なる2色のところから1枚ずつ選ぶ場合
(あ)の場合
ピンク色のところから2か所選ぶ場合を考えます。
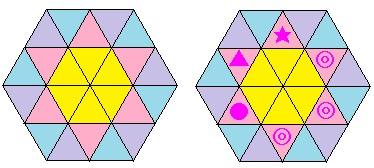
回転によるダブりを防ぐため、まず1か所を固定します(★のところ)。
もう1か所は、正六角形の中心を回転の中心としてその1か所のものを60度、120度、180度回転したところのいずれかのもの(◎のところ)を選ぶことになるので、3通りあります。 ←240度回転したところのもの(●のところ)を選んだ場合、あとから選んだものを120度回転したものが最初に選んだものになり、300度回転したところのもの(▲のところ)を選んだ場合、あとから選んだものを60度回転したものが最初に選んだものになり、回転して同じになる模様になってしまいますね。
他の色についても同様ですね。 ←条件の対等性を利用して作業を減らす!
結局、この場合の模様は
3×4
=12通り
あります。
(い)の場合
4色から異なる2色の選び方は
(4×3)/(2×1)
=6通り
あります。
ピンク色のところから1か所、水色のところから1か所選ぶ場合を考えます。
回転によるダブりを防ぐため、まずピンク色を1か所に固定します(先ほどの★のところ)。
水色のどれを選んでも、回転して同じ模様になることはないので、この場合は6通りあります。
他の2色の組合せについても同様ですね。 ←条件の対等性を利用して作業を減らす!
結局、この場合の模様は
6×6
=36通り
あります。
したがって、模様は全部で
12+36
=48通り
あります。