洛南高校附属中学校2024年算数第6問(解答・解説)
高校で習う余弦定理(角BACが直角の場合は三平方の定理)の証明の際に使われる図を用いた問題です。
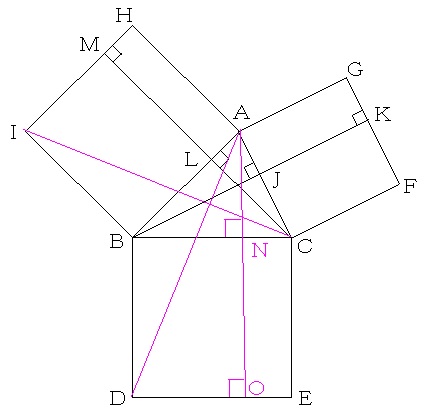 (1)
(1)
三角形ABGと三角形AKGは、底辺(AG)と高さ(GK)が等しいから面積も等しくなります。 ←等積変形したと考えてもいいでしょう。
四角形AJKGの面積は、三角形AKGの面積の2倍だから、18×2=36cm2となります。
(2)
三角形ABGと三角形AHCは合同な三角形です(2辺とその間の角の大きさがそれぞれ等しいから)。 ←「回転+拡大・縮小⇒合同」〜正方形ACFGは正方形AHIBを点Aを中心に回転したものとみなせますね(他の1点でくっつく正方形同士も同様です)。
(1)と同様にすると、四角形AHMLの面積は、36cm2となります。
(3)
(1)、(2)より、正方形AHIBと正方形ACFGの一辺の長さはそれぞれ36/3=12cm、36/4=9cmとなります。
あとは、(1)と同様の作業を行うだけです。
三角形ABDと三角形IBCは合同な三角形です(2辺とその間の角の大きさがそれぞれ等しいから)。
(1)と同様にすると、長方形BDONの面積は、長方形IBLMの面積と等しくなり、12×(12−3)=108cm2となります。
また、三角形ACEと三角形FCBは合同な三角形です(2辺とその間の角の大きさがそれぞれ等しいから)。
(1)と同様にすると、長方形CEONの面積は、長方形CFKJの面積と等しくなり、9×(9−4)=45cm2となります。
したがって、四角形BDECの面積は108+45=153cm2となります。
(参考1)三平方の定理について
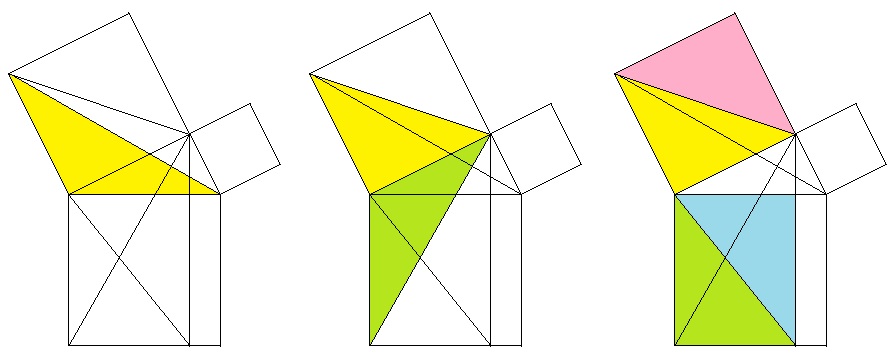
この問題の角BACが直角の場合の三平方の定理の証明(この問題と同様の図を利用した場合の証明法で、実際にはもっと簡明な証明法があります)を図で示しておきます。
上の解説が理解できていれば、言葉がなくてもわかるでしょう。
(参考2)余弦定理について
問題文の図で3cm、4cmの長さをなくしたもので考え、さらに問題文の面積の条件をなくしたもので考えます。
三角形ABCの辺BC、CA、ABの長さをそれぞれa、b、cとします。
三角形ABJと三角形ACLは相似です(2組の角がそれぞれ等しいから)。
共通する角をθとし、直角三角形の1番長い辺に対する、θの角とくっつくもう1つの辺の比率(AJ/AB、AL/AC)をcosθという記号で表すことにします。
AL=b×cosθ、AJ=c×cosθとなり、長方形AHMLの面積はc×b×cosθ、長方形AJKGの面積はb×c×cosθとなります。 ←この2つの長方形の面積が等しいことは計算で自動的に得られましたね。
(3)で示したことにより、
長方形BDONの面積
=長方形IBLMの面積
=c×c−c×b×cosθ
となり、
長方形CEONの面積
=長方形CFKJの面積
=b×b−b×c×cosθ
となり、この2つの長方形の面積の和が正方形BDECの面積となるから、
a×a=b×b+c×c−2×b×c×cosθ (余弦定理(第2余弦定理))
となります。
 (1)
(1)