滝中学校2025年算数第3問(解答・解説)
(1)
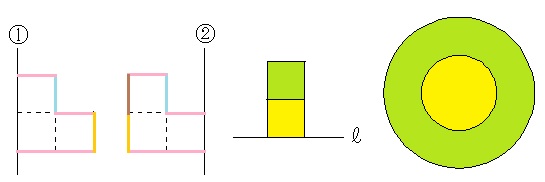
まず、図の黄色の正方形と黄緑色の正方形をそれぞれ直線lの周りに1回転してできる立体の体積比を考えます。
黄色の正方形と図形全体をそれぞれ直線の周りに1回転してできる立体は高さが等しい円柱だから、その体積比は、底面積の比と等しく、(1×1):(2×2)=1:4となります。
黄色の正方形を直線lの周りに1回転してできる立体の体積を1とすると、黄緑色の正方形を直線lの周りに1回転してできる立体の体積は4-1=3となります。
このことを利用して問題を解きます。
AとBの下の部分は同じなので、上の部分の差を求めることになります。
上の部分の正方形は、軸①にとっては、黄色の部分となり、軸②にとっては、黄緑色の部分となるから、Bのほうが
2×2×3.14×2×(3-1)/1
=25.12×2
=50.24cm3
だけ大きくなります。
(2)
底面積部分(図のピンク色の部分を合わせたもの)では、AとBに違いはありません。
側面積部分のうち水色の部分とオレンジ色の部分では、AとBに違いはなく、Bのほうが茶色の部分だけ、つまり
4×2×3.14×2
=50.24cm2
だけ大きくなります。