搶奀拞妛峑俀侽侾俈擭嶼悢戞俇栤乮夝摎丒夝愢乯
乮侾乯
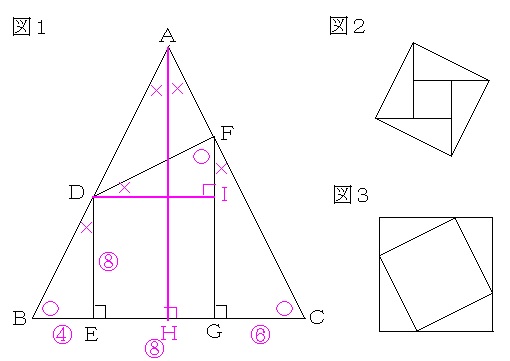
擇摍曈嶰妏宍偑偁傞偺偱丄慄懳徧偺幉俙俫傪堷偒傑偡丅丂仼擇摍曈嶰妏宍偵偍偗傞慄懳徧偺幉偼昿弌偺曗彆慄偺侾偮偱偡丅
俧俠偺挿偝傪嘐偲偍偔偲丄梌偊傜傟偨曈偺斾偺忦審傛傝丄恾偺傛偆偵側傝傑偡丅丂仼俧俠偺挿偝偑俁偺攞悢偵側傝丄俛俤偲俤俧偲俧俠偺挿偝偺崌寁偑嬼悢偵側傞傛偆偵偍偒傑偟偨丅
捈妏嶰妏宍偑偨偔偝傫偁傞偺偱丄妏搙偵婰崋傪偮偗曈偺斾傪僠僃僢僋偡傞偲丄捈妏傪偼偝傓俀曈偺曈偺斾偑俀丗侾偲側傞憡帡側捈妏嶰妏宍偑暋悢搊応偡傞偙偲偑傢偐傝傑偡偹丅
俧俥偺挿偝偼嘐亊俀亖嘖偲側傝丄俛俫偺挿偝偼乮嘋亄嘒亄嘐乯亊侾/俀亖嘓偲側傝丄俙俫偺挿偝偼嘓亊俀亖嘠偲側傝傑偡丅
偙偙偱丄俢俬傪堷偔偲丄嶰妏宍俢俬俥偼丄捈妏傪偼偝傓俀曈偺挿偝偺斾偑嘒丗乮嘖亅嘒乯亖俀丗侾偲側傝丄愭傎偳偺憡帡側捈妏嶰妏宍偲憡帡偱偁傞乮嶰妏宍俢俤俛偲崌摨偱偡偹乯偙偲偑暘偐傝傑偡丅
俙俛偲俙俠偺挿偝偼偲傕偵侾侽亊嘓/嘋亖係俆/俀cm偲側傝丄俥俠偺挿偝偼侾侽亊嘐/嘋亖侾俆cm偲側傝傑偡丅
偟偨偑偭偰丄嶰妏宍俙俢俥偺廃傝偺挿偝偼
丂丂俙俢亄俢俥亄俙俥
丂亖俙俢亄俢俛亄俙俥
丂亖俙俛亄俙俠亅俥俠
丂亖係俆/俀亊俀乕侾俆
丂亖俁侽cm
偲側傝傑偡丅
乮俀乯
俙俥丄俢俥偺挿偝偑偦傟偧傟係俆/俀亅侾俆亖侾俆/俀亖侾俆/俀cm丄侾侽cm偱丄妏俢俥俙偑捈妏偩偐傜丄嶰妏宍俙俢俥偺柺愊偼侾俆/俀亊侾侽亊侾/俀亖俈俆/俀cm2偲側傝傑偡丅
偟偨偑偭偰丄嶰妏宍俙俛俠偺柺愊偼
丂丂嶰妏宍俙俢俥偺柺愊亊俙俛/俙俢亊俙俠/俙俥丂仼偄傢備傞椬曈斾偺張棟偱偡丅
丂亖俈俆/俀亊嘓/乮嘓亅嘋乯亊嘓/乮嘓亅嘐乯丂仼憡帡側捈妏嶰妏宍偺曈偺斾乮乽彫乿偺曈偺斾乯偱張棟偟傑偟偨丅
丂亖俈俆/俀亊俋/俆亊俁
丂亖係侽俆/俀cm2
偲側傝傑偡丅
忋偺夝朄偱偼丄嶰妏宍俙俢俥偑捈妏嶰妏宍乮場傒偵丄桳柤側捈妏嶰妏宍乮曈偺斾偑俁丗係丗俆偺捈妏嶰妏宍乯偵側偭偰偄傑偡偹乯偵側偭偰偄傞偙偲傪棙梡偟偰夝偒傑偟偨偑丄嶰妏宍俢俛俤偺柺愊傪媮傔偰夝偔偙偲傕偱偒傑偡乮乮侾乯偺桿摫偑側偗傟偽偙偺夝朄偱夝偔偙偲偑晛捠偱偟傚偆乯丅
恾俀偐恾俁傪僀儊乕僕偡傟偽偡偖偵媮傔傜傟傞偺偱偤傂傗偭偰傒傑偟傚偆丅丂仼搶奀拞妛峑偱偼夁嫀偵壗夞傕弌偝傟偰偄傑偡丅