東海中学校2019年算数第8問(解答・解説)
(1)
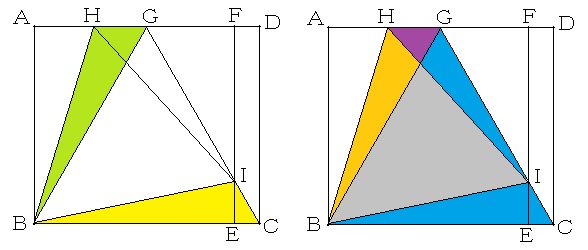
黄色の三角形と黄緑色の三角形は合同だから、 ←回転+拡大・縮小があれば、合同を探すのが基本です(算数オリンピックの問題や最難関中学校の入試問題などでは必須の手法です)。等しい角度と辺にしるしをつければすぐにわかります。
三角形ABHの面積+三角形BEIの面積
=三角形ABHの面積+三角形BCIの面積−三角形ECIの面積
=三角形ABHの面積+三角形BGHの面積−三角形ECIの面積
=三角形AGBの面積−三角形ECIの面積
=長方形ABCDの面積×1/4−三角形ECIの面積
=100×1/4−1
=24cm2
となります。
(2)
面積の差を求める問題なので、同じものを取り除いたりつけ足したりして求めるのが基本です。
三角形BCGの面積−三角形BIHの面積
=水色の三角形の面積の和−オレンジ色の三角形の面積 ←灰色の三角形の面積を取り除きました。
=三角形BCIの面積+三角形HGIの面積−三角形BGHの面積 ←紫色の三角形の面積をつけたしました。
=三角形HGIの面積 ←合同な三角形の面積を取り除きました。
となります。
三角形DGCと三角形ECIは相似で、面積比が25:1=(5×5):(1×1)だから、相似比は5:1となります。 ←三角形DGCの面積=三角形AGBの面積=25cm2となりますね。
三角形BCIは、三角形BCGと底辺が等しく、高さが1/5だから、面積は1/5倍となり、その面積は100×1/2×1/5=10cm2となります。 ←三角形の底辺一定⇒面積比=高さの比
また、三角形HGIは、三角形BGHと底辺が等しく、高さが(5−1)/5=4/5倍だから、面積は4/5倍となり、その面積は10×4/5=8cm2となり、これが答えとなります。