東海中学校2022年算数第4問(解答・解説)
誘導と思われる(1)を無視してメインの(2)の問題を解くと次のようになります。 ←ただし、(2)だけ出題するのであれば本来必要のない直線GEとCEについては利用しました。
変化量(ここでは平均)と「高さの等しい三角形の面積比=底辺の比」を利用して解きます。
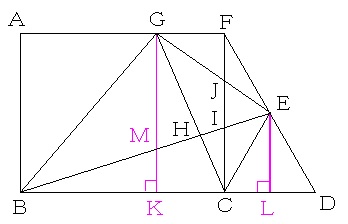
三角形CFG(BFG)の面積を[1]とすると、三角形GBC、三角形GCD、三角形GBDの面積はそれぞれ[1]×3=[3]、[1]×2=[2]、[3]+[2]=[5]となります。
三角形EGCの面積は三角形三角形GCDの面積と三角形CFGの面積の平均となるから、([1]+[2])/2=[3/2]となり、BH:HE=三角形GBCの面積:三角形EGCの面積=[3]:[3/2]=2:1となります。
また、三角形GBEの面積は三角形GBDの面積と三角形BFGの面積の平均となるから、([1]+[5])/2=[3]となります。 ←三角形GBEの面積は三角形GBCの面積と等しくなりますね。
したがって、三角形GBHの面積は
三角形GBEの面積×BH/(BH+HE)
=(6+3)×7×1/2×2/(2+1)
=21cm2
となります。
上の変化量を用いた解法では、長方形の面積と辺の比さえ分かっていれば三角形GBEの面積が求められますね。
なお、誘導に従って解くと次のようになります。
(1)
垂直な補助線GKとELを引きます。
GK=AB=7cm、BK=AG=6cmとなります。
また、三角形ELDと三角形FCDのピラミッド相似(相似比はED:FD=1:(1+1)=1:2)に着目すると、EL=7×1/2=7/2cm、LD=6×1/2=3cm、CL=6−3=3cmとなります。
さらに、三角形MBKと三角形EBLのピラミッド相似(相似比はBK:BL=6:(6+3+3)=1:2)に着目すると、MK=7/2×1/2=7/4cmとなり、MG=7−7/4=21/4cmとなります。
さらにまた、三角形EGMと三角形EJIのピラミッド相似(相似比は、底辺をMG、IJと考えたときの高さの比を考えると、KL:CL=(3+3):3=2:1)に着目すると、IJ=
21/4×1/2=21/8cmとなります。
(2)
三角形BKGと三角形CLEは、角BKG=角CLE=90度で、BK:CL=GK:EL=2:1だから(2辺の辺の比とその間の角がそれぞれ等しいから)、相似で、対応する角度が等しくなり、角GBK=角ECLとなります。
同位角が等しいから、GBとECは平行となります。
三角形HGBと三角形HCEのちょうちょ相似(平行線の錯角に着目すると、2組の角がそれぞれ等しくなるからです。相似比はGB:CE=2:1となります)に着目すると、GH:CH=2:1となります。
したがって、三角形GBHの面積は
三角形BCGの面積×GH/(GH+CH)
=9×7×1/2×2/(2+1)
=21cm2
となります。