搶奀拞妛峑俀侽俀俀擭嶼悢戞俇栤乮夝摎丒夝愢乯
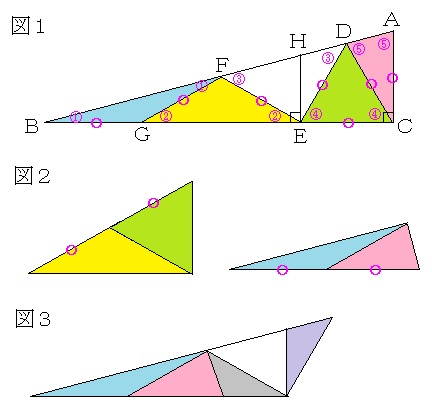
妏俛偺戝偒偝傪嘆偲偟丄擇摍曈嶰妏宍偲嶰妏宍偺奜妏偵拝栚偟丄妏偺戝偒偝傪彂偄偰偄偔偲丄恾侾偺傛偆偵側傝傑偡丅
嘋偑俇侽搙偵憡摉偡傞偐傜丄嘆丄嘇丄嘊丄嘍偼偦傟偧傟侾俆搙丄俁侽搙丄係俆搙丄俈俆搙偲側傝傑偡丅
榓偑侾俉侽搙偵側傞妏傪堄幆偟側偑傜丄摍偟偄挿偝偺曈傪偔偭偮偗傞偲丄恾俀偺傛偆偵側傝丄墿怓偺嶰妏宍偲墿椢怓偺嶰妏宍丄悈怓偺嶰妏宍偲僺儞僋怓偺嶰妏宍偼丄偦傟偧傟掙曈偲崅偝偑摍偟偄偐傜丄柺愊偑摍偟偔側傝傑偡丅
偙偺偙偲偲嶰妏宍俥俛俤偺柺愊偲嶰妏宍俥俤俫偺柺愊偺嵎偑俆cm2偱偁傞偙偲偐傜丄媮傔傞柺愊偺嵎偼丄敄巼怓偺嶰妏宍偺柺愊偵俆傪壛偊偨傕偺偲側傝傑偡丅
偙偙偱丄嶰妏宍俥俛俤偺柺愊偲嶰妏宍俥俤俫偺柺愊偺嵎偑俆cm2偲偄偆忦審傪暘愅偟傑偡丅
丂丂嶰妏宍俥俛俤偺柺愊亅嶰妏宍俥俤俫偺柺愊
丂亖乮嶰妏宍俥俛俤偺柺愊亄敄巼怓偺嶰妏宍偺柺愊乯亅乮嶰妏宍俥俤俫偺柺愊亄敄巼怓偺嶰妏宍偺柺愊乯丂仼摨偠傕偺傪偮偗懌偟傑偟偨丅柺愊偺嵎傪峫偊傞応崌丄摨偠傕偺傪庢傝彍偄偨傝偮偗懌偟偨傝偟偰峫偊傞偺偑婎杮偱偡偹丅
丂亖乮嶰妏宍俥俛俤偺柺愊亄敄巼怓偺嶰妏宍偺柺愊乯亅捈妏擇摍曈嶰妏宍俢俥俤偺柺愊
丂亖乮悈怓偺嶰妏宍偺柺愊亄僺儞僋怓偺嶰妏宍偺柺愊亄奃怓偺嶰妏宍偺柺愊亄敄巼怓偺嶰妏宍偺柺愊乯亅捈妏擇摍曈嶰妏宍俢俥俤偺柺愊
丂亖奃怓偺嶰妏宍偺柺愊亄敄巼怓偺嶰妏宍偺柺愊丂仼摨偠傕偺傪庢傝彍偒傑偟偨丅栤戣暥偵梌偊傜傟偨摍偟偄挿偝傪乑偲偡傞偲丄悈怓偺嶰妏宍偺柺愊亄僺儞僋怓偺嶰妏宍偺柺愊偼丄嶰妏掕婯乮惓嶰妏宍偺敿暘偺傕偺乯偺曈偺挿偝偺斾傪棙梡偡傞偲丄乑亊乮乑亊侾/俀乯亊侾/俀亊俀偲側傝丄捈妏擇摍曈嶰妏宍俢俥俤偺柺愊偼乑亊乑亊侾/俀偲側傝丄摍偟偔側傝傑偡偹丅
丂亖敄巼怓偺嶰妏宍亊俀丂仼奃怓偺嶰妏宍偲敄巼怓偺嶰妏宍偺摍偟偄曈偲偦偺椉抂偺妏傪僠僃僢僋偡傟偽丄俀偮偺嶰妏宍偑崌摨偱偁傞偙偲偑傢偐傝傑偡丅
偲側傝丄偙傟偑俆cm2偵憡摉偡傞偐傜丄媮傔傞柺愊偺嵎偼丄
丂丂俆/俀亄俆
丂亖侾俆/俀cm2
偲側傝傑偡丅