東海中学校2024年算数第4問(解答・解説)
直角三角形がたくさんあるので、角度に記号をつけると、三角形ABEと三角形BCFが合同であり、点Fが辺CDの真ん中の点であることがすぐにわかりますね。
過去問(東海中学校2018年算数第4問)を少しアレンジした問題ですね。
上の過去問の解説で紹介した解き方とは異なる解き方で解いてみます。
(2)
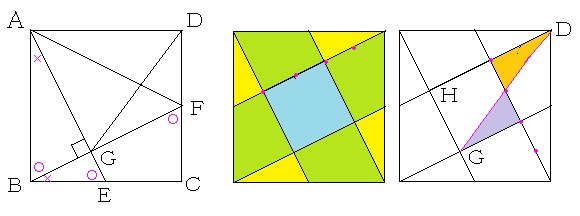
正方形の各辺の真ん中の点と正方形の各頂点を図のように結びます。
黄色の直角三角形と黄色と黄緑色を合わせた直角三角形は相似で、相似比が1:2だから、図のピンク色の・は斜辺(直角の向かいの辺)を5等分する点となります。 ←因(ちな)みに、水色の正方形と黄色と黄緑色を合わせた直角三角形の面積は等しくなります。
この図において、問題文の図のDGに相当する線を引くと、紫色の直角三角形とオレンジ色の三角形は合同となります。 ←ちょうちょ相似で、相似比が1:1だからです。
したがって、オレンジ色の直角三角形と黄色の直角三角形は合同となります。 ←直角を挟む辺の比が1:2で、2に相当する辺を共有するからです。
結局、DGの長さはDAの長さと等しくなるから、DGの長さは24cmとなります。 ←AGの真ん中の点をHとすると、三角形DGHと三角形DAHは合同となりますね。
(1)
三角形ABGと三角形AGFは、高さが等しく(AG)、底辺の比がBG:GF=2:3だから、面積の比も2:3となります。
三角形AGDの面積は三角形DAH(三角形ABGと合同)の面積の2倍となります。
したがって、三角形AGFと三角形AGDの面積の比=3:(2×2)=3:4となります。