東海中学校2024年算数第8問(解答・解説)
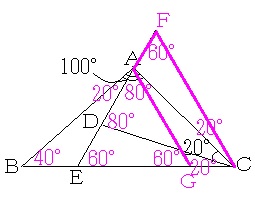
まず、二等辺三角形に着目し角度を書き込みます。
60度、20度、40度、100度の角度の存在から、正三角形を作出することを考えますが、その際、線対称をフル活用します。
三角形CDEを二等辺三角形CADの線対称の軸に関して折り返すと、三角形CAFとなり、三角形CFEは正三角形となります。
三角形ABEを二等辺三角形ABCの線対称の軸に関して折り返すと、三角形ACGとなり、三角形AEGは正三角形となります。
CGの長さもFAの長さも、三角形CFEの1辺の長さから三角形AEGの1辺の長さを引いたものになるから、BE、CG、FA、EDの長さはすべて等しくなりますね。
BCとADの長さの差は、BEとEFの長さの合計からADの長さを引いたもの、つまりBEの長さの3倍となるから、BEの長さは5/3cmとなります。