東海中学校2025年算数第3問(解答・解説)
(1)と(2)を同じ解法で解きます。
消去算としても処理できますが、てんびん算として処理します。
(1)
Aの個数が2倍、Bの個数が1/3倍になって、合わせた個数が変わらない(1倍)ということですね。
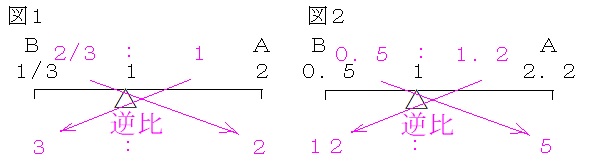
図1より、今年のAの個数は
10×2/(3+2)×2
=8個
となります。
なお、合計個数が少ないので、下のようにしてもよいでしょう。
昨年のBの個数は3の倍数だから、昨年のBとAの個数の組合せは
B 3個 6個 9個
A 7個 4個 1個
となります。
このうちA7個の場合は、2倍すると10個を超えて論外で、B9個の場合、9×1/3+1×2<10となり、条件を満たしません。
残りの場合は条件を満たす(6×1/3+4×2=10)から、答えは8個とあります。
(2)
Aの代金総額が1.1×2=2.2倍、Bの代金総額が1.5×1/3=0.5倍になって、代金総額が変わらない(1倍)ということですね。
図2より、今年のBの値段は
20400×12/(12+5)×1/6×1.5 ←うまく約分できますね。
=3600円
となります。