東海中学校2025年算数第7問(解答・解説)
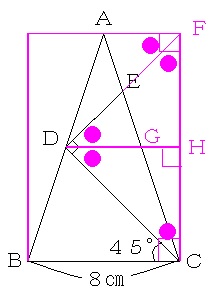
図のように、二等辺三角形を長方形の中にはめ込みます。
AFの長さは、BCの長さの半分、つまり8/2=4cmとなり、DHの長さは、AFの長さとBCの長さの平均、つまり(4+8)/2=6cmとなり、DGの長さは、三角形ABCと三角形ADGのピラミッド相似に着目すると、8/2=4cmとなります。
また、図の●はすべて45度となるから、三角形CFDは直角二等辺三角形となり、CFの長さは、DHの長さの2倍、つまり6×2=12cmとなり、三角形CFDの面積は12×6×1/2=36cm2となります。
三角形AEFと三角形GEDは合同だから、FE=DEとなり、三角形CDEの面積は三角形CFDの面積の半分、つまり18cm2となります。