巐揤墹帥拞妛峑俀侽侽俀擭嶼悢俛戞俁栤乮夝摎丒夝愢乯
師偺抦幆傪棙梡偡傟偽丄娙扨偵夝偗傑偡丅
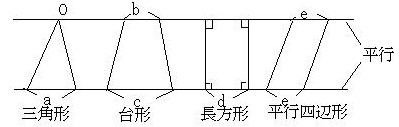
乮暯峴慄偲柺愊斾乯
壓偺恾偺柺愊斾偼丄偄偢傟傕乽忋掙亄壓掙乿偺斾偱張棟偱偒傑偡乮挿曽宍傕暯峴巐曈宍傕戜宍偩偐傜丄嵍偺俀偮偱偡傋偰張棟偱偒傑偡丅傑偨丄嶰妏宍傪忋掙侽偺戜宍偲峫偊傞偲丄偡傋偰傪戜宍偲偟偰張棟偱偒傑偡偹乯丅
柺愊斾偼
丂丂乮a亄侽乯丗乮倐亄們乯丗乮倓亄倓乯丗乮e亄e乯
偲側傝傑偡丅
偝偰丄栤戣傪夝偄偰傒傑偟傚偆丅
丂丂俛俤
丂亖乮俙俢亄俛俠乯亊嶰妏宍俙俛俤偺柺愊/暯峴巐曈宍俙俛俠俢偺柺愊
丂亖俉亊俀亊俁/侾侽
丂亖係俉/侾侽丂仼暘曣偑侾丄侾侽丄侾侽侽丄丒丒丒側傜彫悢偵側偍偟傗偡偄偺偱丄偁偊偰栺暘偟傑偣傫丅
丂亖係丏俉cm
偟偨偑偭偰丄
丂丂俤俠
丂亖俛俠亅俛俤
丂亖俉亅係丏俉
丂亖俁丏俀cm
側偍丄師偺傛偆偵偟偰傕偄偄偱偟傚偆丅寢嬊偼丄摨偠偙偲偱偡偑丒丒丒
暯峴巐曈宍俙俛俠俢偺柺愊傪嘔偲偡傞偲丄
丂丂戜宍俙俤俠俢偺柺愊
丂亖暯峴巐曈宍俙俛俠俢偺柺愊亊俈/侾侽
丂亖嘔亊俈/侾侽
丂亖嘑
偲側傝丄
丂丂嶰妏宍俙俛俤偺柺愊
丂亖嘔亅嘑
丂亖嘊
偲側傝傑偡丅
傑偨丄
丂丂嶰妏宍俙俛俠偺柺愊
丂亖暯峴巐曈宍俙俛俠俢偺柺愊亊侾/俀
丂亖嘔亊侾/俀
丂亖嘍
偩偐傜丄
丂丂嶰妏宍俙俤俠偺柺愊
丂亖嘍亅嘊
丂亖嘇
偲側傝傑偡丅
嶰妏宍俙俤俠偲嶰妏宍俙俛俠偼崅偝偑摍偟偄偺偱丄掙曈偺斾偼
丂丂俤俠丗俛俠丂丂丂乮嶰妏宍偺乯崅偝堦掕仺掙曈偺斾亖柺愊斾
丂亖嘇丗嘍
偲側傝傑偡丅
俛俠亖俙俢亖俉cm偩偐傜丄俤俠偺挿偝偼
丂丂俉亊俀/俆
丂亖侾俇/俆乮亖俁丏俀乯cm
偲側傝傑偡丅