巐揤墹帥拞妛峑俀侽俀俁擭嶼悢戞俁栤乮夝摎丒夝愢乯
乮侾乯
懳徧惈偵傛傝丄惓曽宍俙俛俠俢偺懳妏慄俙俠傪寢傇偲俁揰俙丄俧丄俠偼堦捈慄偵側傝傑偡丅
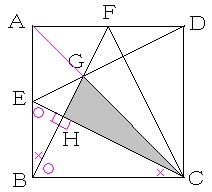
嶰妏宍俛俧俠偲嶰妏宍俥俧俙偼憡帡乮憡帡斾偼俛俠丗俥俙亖俀丗侾乯偩偐傜丄俛俧丗俧俥亖俀丗侾偲側傝傑偡丅
乮俀乯
捈妏嶰妏宍俛俠俤偲捈妏嶰妏宍俙俛俥偑崌摨偱偁傞偙偲偵拝栚偟妏搙偵婰崋傪晅偗傞偲丄捈妏嶰妏宍俛俠俤偲捈妏嶰妏宍俫俛俤偲捈妏嶰妏宍俫俠俛偼憡帡乮曈偺斾偼丄彫丗拞亖俤俛丗俛俠亖侾丗俀乯偲側傞偙偲偑傢偐傝傑偡丅
俤俫亖嘆偲偡傞偲丄俛俫亖嘆亊俀亖嘇偲側傝丄俠俫亖嘇亊俀亖嘋偲側傝丄俛俥亖俠俤亖嘆亄嘋亖嘍偲側傝傑偡丅
偟偨偑偭偰丄俛俫丗俫俥亖嘇丗乮嘍亅嘇乯亖俀丗俁偲側傝傑偡丅
乮俁乯
俛俥亖侾俆偲偡傞偲丄丂仼俀亄侾亖俁偲俀亄俁亖俆偺嵟彫岞攞悢偱偍偒傑偟偨丅
丂丂俛俫丗俫俧丗俧俥
丂亖乮侾俆亊俀/俆乯丗俫俧丗乮侾俆亊侾/俁乯
丂亖俇丗乮侾俆亅俇亅俆乯丗俆
丂亖俇丗係丗俆
偲側傝傑偡丅
偟偨偑偭偰丄嶰妏宍俠俧俫偺柺愊偼
丂丂嶰妏宍俠俥俛偺柺愊亊俫俧/俛俥丂仼嶰妏宍偺崅偝堦掕佀柺愊斾亖掙曈偺斾
丂亖俁侽亊侾/俀亊係/侾俆
丂亖係cm2
偲側傝傑偡丅
側偍丄乮俁乯偩偗傪夝偔偺偱偁傟偽丄惓曽宍俙俛俠俢偺懳妏慄傪寢傃丄嶰妏宍俙俤俧偲嶰妏宍俠俢俧偺憡帡乮憡帡斾偼俙俤丗俠俢亖侾丗俀乯偐傜俢俧丗俧俤亖俀丗侾偲媮傔丄乮俀乯偲摨條偵偟偰乮偁傞偄偼丄捈妏嶰妏宍俫俛俤偲捈妏嶰妏宍俫俠俛偺柺愊斾亖乮侾亊侾乯丗乮俀亊俀乯亖侾丗係偲側傞偙偲傪棙梡偟偰乯丄俤俫丗俫俠亖侾丗係傪媮傔偨屻丄嶰妏宍俠俧俫偺柺愊亖嶰妏宍俤俠俢偺柺愊亊俤俧/俤俢亊俫俠/俠俤亖俁侽亊侾/俀亊侾/乮侾亄俀乯亊係/乮侾亄係乯亖係cm2偲偟偨傎偆偑妝偱偟傚偆丅
